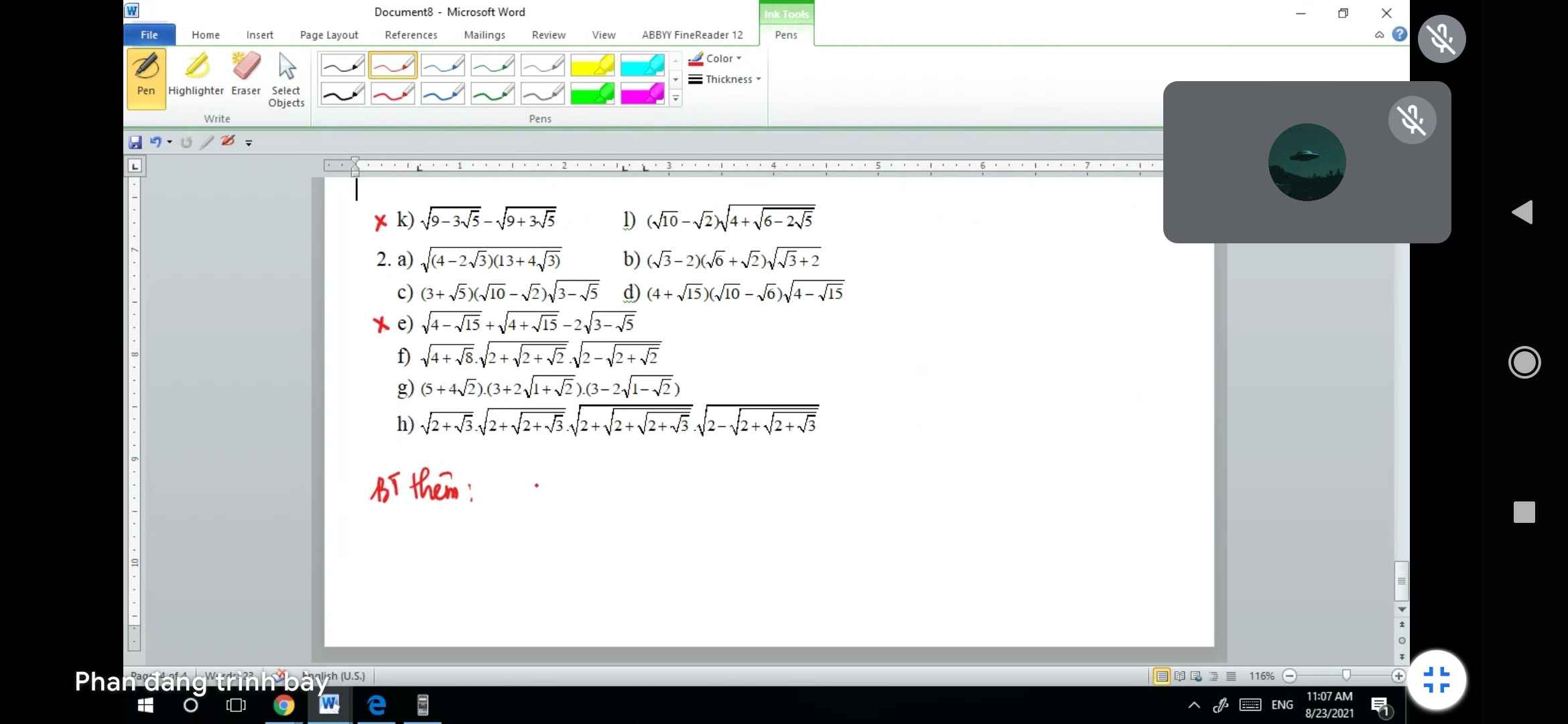
giúp mik câu d) vs e) ddc k mn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NY
2
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 8 2021
\(\sqrt{9-3\sqrt{5}}-\sqrt{9+3\sqrt{5}}=\dfrac{1}{\sqrt{2}}\left(\sqrt{18-6\sqrt{5}}-\sqrt{18+6\sqrt{5}}\right)\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{\left(\sqrt{15}-\sqrt{3}\right)^2}-\sqrt{\left(\sqrt{15}+\sqrt{3}\right)^2}\right)\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{15}-\sqrt{3}-\sqrt{15}-\sqrt{3}\right)=-\dfrac{2\sqrt{3}}{\sqrt{2}}=-\sqrt{6}\)
\(\sqrt{4-\sqrt{15}}+\sqrt{4+\sqrt{15}}-2\sqrt{3-\sqrt{5}}\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{8-2\sqrt{15}}+\sqrt{8+2\sqrt{15}}-2\sqrt{6-2\sqrt{5}}\right)\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{\left(\sqrt{5}-\sqrt{3}\right)^2}+\sqrt{\left(\sqrt{5}+\sqrt{3}\right)^2}-2\sqrt{\left(\sqrt{5}-1\right)^2}\right)\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{5}-\sqrt{3}+\sqrt{5}+\sqrt{3}-2\left(\sqrt{5}-1\right)\right)\)
\(=\dfrac{2}{\sqrt{2}}=\sqrt{2}\)
24 tháng 8 2021
k: Ta có: \(\sqrt{9-3\sqrt{5}}-\sqrt{9+3\sqrt{5}}\)
\(=\dfrac{\sqrt{18-6\sqrt{5}}-\sqrt{18+6\sqrt{5}}}{\sqrt{2}}\)
\(=\dfrac{\sqrt{15}-\sqrt{3}-\sqrt{15}-\sqrt{3}}{\sqrt{2}}\)
\(=-\sqrt{6}\)
12 tháng 2 2023
d: Xét tứ giác NKCM có
NK//CM
NK=CM
=>NKCM là hình bình hành
=>NC cắt KM tại trung điểm của mỗi đường
=>M,I,K thẳng hàng
3 tháng 8 2016
bạn tự vẽ hình nha
a) góc ACB=góc ECN (đối đỉnh)
góc ABC=góc ACB(tam giác ABC cân )
--> góc ABC=góc ECN
xét 2 tam giác BDM và CEN có:
cạnh BD=cạnh EC(gt)
góc BDM=góc CEN(=90độ)
góc MBC=góc ECN(chứng minh trên )
--> 2 tam giác BDM=CEN(g.c.g)
--> DM=EN(2 cạnh tương ứng)
c)xét 2 tam giác AOB và AOC có:
AB=AC(tam giác ABC cân)
góc BAO=góc CAO(tia OA là p.giác của góc A)
cạnh AO chung
--> 2 tam giác AOB=AOC(c.g.c)
LL
13 tháng 12 2021
- Đó là chiếc lá thường xuân do cụ Bơ-men đã vẽ với mong muốn truyền thêm niềm tin và hi vọng để Giôn-xi chiến thắng bệnh tật.
13 tháng 12 2021
Bạn tham khảo một đoạn cảm nhận trích từ trang Văn học và tuổi xanh nhé.
Những chiếc lá thường xuân, theo quy luật sinh tồn của tạo hóa, từng chiếc một theo mùa đông rét mướt rụng đi. Chiêc lá cuối cùng sót lại không phải bởi cây ấy là cây thường xuân, không phải bởi lá ấy là lá thường xuân mà bởi nét vẽ tài hoa của ông lão Bơ-men làm trường xuân lá ấy. Cây tuy là thường xuân cũng không giữ được lá của mình. Người tuy là hữu hạn nhưng lại giữ được lá. Vậy ra điều duy nhất để giữ lá kia ở lại trên dương thế này là tấm lòng. Con người dẫu có chết nhưng tấm lòng kia vẫn lưu tồn muôn thuở.
Tấm lòng đã thăng hoa thành nghệ thuật. Và nghệ thuật đã mang thiên chức cứu người. Chiếc lá ấy là kiệt tác của Bơ-men, người “luôn ấp ủ dự định vẽ một bức kiệt tác, nhưng vẫn chưa bắt đầu”.
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
21 tháng 12 2023
(d) cắt Ox nên ta có phương trình hoành độ:
(k - 1)\(x\) - 4 = 0
(k - 1)\(x\) = 4
\(x\) = \(\dfrac{4}{k-1}\) (k ≠ 1)
Theo bài ra ta có:
\(\dfrac{4}{k-1}\) ≤ 1
⇒ \(\dfrac{4}{k-1}\) - 1 ≤ 0
\(\dfrac{4-k-1}{k-1}\) ≤ 0
\(\dfrac{5-k}{k-1}\) ≤ 0
A = \(\dfrac{5-k}{k-1}\) ≤ 0
Lập bảng ta có:
| k | 1 5 |
| 5 - k | + + 0 - |
| k - 1 | - 0 + + |
| \(\dfrac{5-k}{k-1}\) | - || + 0 - |
Theo bảng trên ta có: 1 < k hoặc k ≥ 5
Kl:...
QN
vẽ hình giúp mik nha mik cảm ơn rất rất nhiều
1
29 tháng 7 2023
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
=>AB/HB=AC/HA
=>AB*HA=HB*AC
b: AH=căn 5^2-3^2=4cm
BI là phân giác
=>HI/HB=IA/AB
=>HI/3=IA/5=(HI+IA)/(3+5)=0,5
=>HI=1,5cm; IA=1,5cm
a: Xét (O) có
MD,MA là các tiếp tuyến
Do đó: MD=MA và MO là phân giác của góc DMA
Xét (O') có
MA,ME là các tiếp tuyến
Do đó: MA=ME và MO' là phân giác của góc AME
Ta có: MD=MA
MA=ME
Do đó: MD=ME
=>M là trung điểm của DE
=>DE=2DM
mà DM=MA
nên DE=2MA
Ta có; MO là phân giác của góc DMA
=>\(\hat{DMA}=2\cdot\hat{OMA}\)
MO' là phân giác của góc AME
=>\(\hat{AME}=2\cdot\hat{AMO^{\prime}}\)
Ta có: \(\hat{DMA}+\hat{EMA}=180^0\) (hai góc kề bù)
=>\(2\left(\hat{OMA}+\hat{O^{\prime}MA}\right)=180^0\)
=>\(2\cdot\hat{O^{\prime}MO}=180^0\)
=>\(\hat{O^{\prime}MO}=90^0\)
b: Xét ΔMO'O vuông tại M có MA là đường cao
nên \(MA^2=OA\cdot O^{\prime}A=6\cdot2=12\)
=>\(MA=2\sqrt3\left(\operatorname{cm}\right)\)
Xét ΔMAO vuông tại A có tan MOA\(=\frac{MA}{AO}=\frac{2\sqrt3}{6}=\frac{\sqrt3}{3}\)
nên \(\hat{MOA}=30^0\)
Xét (O) có
MD,MA là các tiếp tuyến
Do đó: OM là phân giác của góc AOD
=>\(\hat{AOD}=2\cdot\hat{AOM}=2\cdot30^0=60^0\)
c: Xét ΔDAE có
AM là đường trung tuyến
\(AM=\frac{DE}{2}\)
Do đó: ΔDAE vuông tại A
=>DA⊥EA
Xét (O) có
ΔDAF nội tiếp
DF là đường kính
Do đó: ΔDAF vuông tại A
=>DA⊥AF
Ta có: DA⊥AF
DA⊥ AE
mà AF,AE có điểm chung là A
nên A,F,E thẳng hàng
d: Xét (O) có
ΔBDA nội tiếp
BA là đường kính
Do đó: ΔBDA vuông tại D
=>AD⊥BK tại D
Xét (O') có
ΔAEC nội tiếp
AC là đường kính
Do đó: ΔAEC vuông tại E
=>AE⊥KC tại E
Xét tứ giác KDAE có \(\hat{KDA}=\hat{KEA}=\hat{DAE}=90^0\)
nên KDAE là hình chữ nhật
=>KA cắt DE tại trung điểm của mỗi đường
mà M là trung điểm của DE
nên M là trung điểm của KA
=>K,M,A thẳng hàng
e: Xét ΔKAB vuông tại A có AD là đường cao
nên \(KD\cdot KB=KA^2\)
mà KA=DE(ADKE là hình chữ nhật)
nên \(KD\cdot KB=DE^2\)