Vật AB cao 2cm đặt vuông góc với trục chính của thấu kính hội tụ cho ảnh A'B' cao 4cm.Tiêu cự thấu kính là f=20 cm.Xác định vị trí của vật và ảnh
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Khoảng cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{20}=\dfrac{1}{30}+\dfrac{1}{d'}\Leftrightarrow d'=60cm\)
Độ cao ảnh:
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{2}{h'}=\dfrac{30}{60}\Rightarrow h'=4cm\)

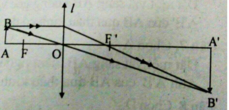
Ta có hình vẽ 2, xét tam giác đồng dạng OAB và OA’B’ ta được công thức:
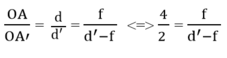
Mặt khác d’ = 2d/4 = 2.10/4 = 5(cm)
Vậy f/(5-f ) = 2 ⇔ f = 10 – 2f => f = 10/3 (cm)

(đề bài), ...và cách thấu kính 12cm à (hình anh tự vẽ )
\(=>d< f\left(12cm< 20cm\right)\)=>ảnh tạo bới vật AB qua thấu kính hội tụ là ảnh ảo , lớn hơn vật và cùng chiều vật
\(=>\dfrac{1}{f}=\dfrac{1}{d}-\dfrac{1}{d'}=>\dfrac{1}{20}=\dfrac{1}{12}-\dfrac{1}{d'}=>d'=30cm\)
=>ảnh cách tk 30cm
\(=>\dfrac{h}{h'}=\dfrac{d}{d'}=>\dfrac{2}{h'}=\dfrac{12}{30}=>h'=5cm\)
=>ảnh A'B' cao 5cm
\(=>\)khoảng cách giữa ảnh với vật d+d'=42cm

AB = 2cm
OA = 15cm
OF = 10cm
a. Hình vẽ tham khảo ảnh
b. Ta có 1/A'O = 1/OF - 1/AO = 1/10 - 1/15 = 1/30 hay A'O = 30cm
Vì A'B'/AB = A'O/AO nên A'B' = (AB.A'O)/AO = (2.30)/15 = 4cm
Vậy ảnh cao 4cm và cách thấu kính một đoạn 30cm
(Cách chứng minh như trong hình vẽ)

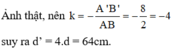
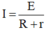
\(k=\dfrac{\overline{A'B'}}{\overline{AB}}=-\dfrac{d'}{d}=2\Rightarrow d'+2d=0\)
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Leftrightarrow\dfrac{1}{f}=\dfrac{d'+d}{dd'}\Leftrightarrow f\left(d'+d\right)=dd'\)
\(\Leftrightarrow20\left(-2d+d\right)=d.\left(-2\right)d\)
\(\Leftrightarrow2d^2-20d=0\Leftrightarrow d=10\left(cm\right)\Rightarrow d'=-20\left(cm\right)\)