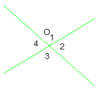
Cho 2 đường thẳng a và b cắt nhau tại O. Tính các góc O1,O2,O3,O4 nếu O1+O3=O2+O4.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 1 2022
\(\widehat{O_1}=\widehat{O_3}=110^0;\widehat{O_2}=\widehat{O_4}=70^0\)
12 tháng 9 2021
bài1
Giả sử trong hình bên, hai đường thẳng xx’ và yy’ cắt nhau tại O, góc xOy bằng 60o
Ta có: ∠xOy = ∠x’Oy'(hai góc đối đỉnh)
Suy ra ∠x’Oy’=60o.
∠xOy + ∠x’Oy’= 180o (hai góc kề bù)
⇒ ∠x’Oy’ = 180o – ∠xOy = 180o – 60o = 120o
∠xOy’ = ∠x’Oy(hai góc đối đỉnh)
⇒∠x’Oy=120o
18 tháng 7 2021
Ta có: ∠O1 + ∠O2 = 1800 (2 góc kề bù)
Mà ∠O2 − ∠O1 =300
⇒ 2.∠O2 = 1800 + 300 = 2100
⇒ ∠O2 = 2100:2 = 1050 ⇒ ∠O2 = ∠O4 = 1050 (đối đỉnh)
⇒ ∠O1 = 1800 −1050 = 750 ⇒ ∠O1 = ∠O3 = 750 (đối đỉnh)
AB
18 tháng 7 2021
Hai đường thẳng cắt nhau tạo thành 4 góc O1, O2, O3, O4. Tính các góc còn lại biết O2-O1=30
Giải:
Ta có: ∠O1 + ∠O2 = 1800 (2 góc kề bù)
Mà ∠O2 − ∠O1 =300
⇒ 2.∠O2 = 1800 + 300 = 2100
⇒ ∠O2 = 2100:2 = 1050 ⇒ ∠O2 =∠O4 = 1050 (đối đỉnh)
⇒ ∠O1 = 1800 −1050 = 750 ⇒ ∠O1 = ∠O3 = 750 (đối đỉnh)
CM
8 tháng 11 2017
Cho hình vẽ. Tính O 1 ^ , O 2 ^ , O 3 ^ , O 4 ^ nếu biết:
a) Vì O 1 ^ + O 2 ^ = 180 0 ( Hai góc kề bù) mà O 1 ^ = 1 2 O 2 ^ nên
1 2 O 2 ^ + O 2 ^ = 180 0 ⇒ 3 2 O 2 ^ = 180 0 ⇒ O 2 ^ = 180 0 .2 3 = 120 0
O 1 ^ = 1 2 O 2 ^ ⇒ O 1 ^ = 1 2 .120 0 = 60 0
Vậy O 1 ^ = O 3 ^ = 60 0 ; O 2 ^ = O 4 ^ = 120 0
b) Vì O 1 ^ + O 2 ^ = 180 0 ( Hai góc kề bù) mà O 2 ^ − O 1 ^ = 40 0
⇒ 2 O 2 ^ = 220 0 ⇒ O 2 ^ = 110 0
O 2 ^ − O 1 ^ = 40 0 ⇒ 120 0 − O 1 ^ = 40 0 ⇒ O 1 ^ = 70 0
Vậy O 1 ^ = O 3 ^ = 70 0 ; O 2 ^ = O 4 ^ = 110 0
c) O 1 ^ + O 3 ^ = 130 0 Mà O 1 ^ = O 3 ^ ( Đối đỉnh) nên O 1 ^ = O 3 ^ = 130 0 : 2 = 65 0
O 2 ^ = O 4 ^ = 180 0 − 65 0 = 115 0 ( Hai góc kè bù)
d) O 1 ^ + O 2 ^ + O 3 ^ = 250 0
Vì O 1 ^ + O 2 ^ = 180 0 ( Hai góc kề bù) nên O 3 ^ = 250 0 − 180 0 = 70 0 .
Do đó O 1 ^ = O 3 ^ = 70 0 ( Đối đỉnh)
O 2 ^ = 180 0 − 70 0 = 110 0 . Suy ra O 4 ^ = O 2 ^ = 110 0 ( Đối đỉnh)
e) O 1 ^ + O 3 ^ = 1 2 ( O 2 ^ + O 4 ^ )
Mà O 1 ^ = O 3 ^ ( Đối đỉnh) , O 4 ^ = O 2 ^ ( Đối đỉnh)
Suy ra 2 O 1 ^ = 1 2 .2 O 2 ^ ⇒ 2 O 1 ^ = O 2 ^
Vì O 1 ^ + O 2 ^ = 180 0 ( Hai góc kề bù). Suy ra O 1 ^ + 2 O 1 ^ = 180 0 ⇒ O 1 ^ = 60 0
O 1 ^ = O 3 ^ = 60 0 ; O 2 ^ = 2 O 1 ^ = 60 0 .2 = 120 0 ⇒ O 4 ^ = O 2 ^ = 120 0
17 tháng 7 2019
O 1 2 3 4
Giải: a) Ta có: \(\widehat{O_1}=\widehat{O_3}\) (đối đỉnh)
mà \(\widehat{O_1}+\widehat{O_3}=140^0\)
=> \(\widehat{O_1}=\widehat{O_3}=70^0\)
Ta lại có: \(\widehat{O_1}+\widehat{O_2}=180^0\)
=> \(\widehat{O_2}=180^0-\widehat{O_1}=180^0-70^0=110^0\)
=> \(\widehat{O_2}=\widehat{O_4}=110^0\) (đối đỉnh)
b) Ta có: \(\widehat{O_1}+\widehat{O_2}+\widehat{O_3}=240^0\)
mà \(\widehat{O_1}+\widehat{O_2}=180^0\)(kề bù)
=> \(\widehat{O_3}=240^0-\left(\widehat{O_1}+\widehat{O_2}\right)=240^0-180^0=60^0\)
=> \(\widehat{O_3}=\widehat{O_1}=60^0\) (đối đỉnh)
=> \(\widehat{O_2}=180^0-\widehat{O_1}=180^0-60^0=120^0\)
=> \(\widehat{O_2}=\widehat{O_4}=120^0\) (đối đỉnh)
c) Ta có: \(\widehat{O_1}+\widehat{O_2}=180^0\) (kề bù)
mà \(\widehat{O_2}-\widehat{O_1}=30^0\)
=> \(2.\widehat{O_2}=180^0+30^0=210^0\)
=> \(\widehat{O_2}=210^0:2=105^0\) => \(\widehat{O_2}=\widehat{O_4}=105^0\)(đối đỉnh)
=> \(\widehat{O_1}=180^0-105^0=75^0\) => \(\widehat{O_1}=\widehat{O_3}=75^0\) (đối đỉnh)
d) Ta có: \(\widehat{O_1}+\widehat{O_2}=180^0\) (kề bù)
=> \(\widehat{O_1}+2.\widehat{O_1}=180^0\)
=> \(3.\widehat{O_1}=180^0\)
=> \(\widehat{O_1}=180^0:3=60^0\) => \(\widehat{O_1}=\widehat{O_3}=60^0\) (đối đỉnh)
=> \(\widehat{O_2}=180^0-60^0=120^0\) => \(\widehat{O_2}=\widehat{O_4}=120^0\) (Đối đỉnh)
e) Ta có: \(\widehat{O_1}+\widehat{O_2}=180^0\) (kề bù)
=> \(\widehat{O_2}=180^0-\widehat{O_1}=180^0-75^0=105^0\)
=> \(\widehat{O_2}=\widehat{O_4}=105^0\) (đối đỉnh)
Ta lại có: \(\widehat{O_1}=\widehat{O_3}\) (đối đỉnh)
Mà \(\widehat{O_1}=75^0\) => \(\widehat{O_3}=75^0\)
24 tháng 9 2021
\(\left\{{}\begin{matrix}\widehat{O_2}+\widehat{O_3}=180^0\left(kề.bù\right)\\\widehat{O_2}-\widehat{O_3}=12^0\left(kề.bù\right)\end{matrix}\right.\Rightarrow\widehat{O_2}=\left(180^0+12^0\right):2=96^0;\widehat{O_3}=84^0\)
\(\widehat{O_3}=\widehat{O_1}=84^0;\widehat{O_2}=\widehat{O_4}=96^0\left(các.cặp.góc.đối.đỉnh\right)\)
18 giờ trước (8:54)
a) Khi \(o_3=55^{\circ}\)
- Khi hai đường thẳng cắt nhau tại điểm \(O\), ta có bốn góc: \(o_1,o_2,o_3,o_4\).
- Các góc đối diện với nhau là bằng nhau, tức là:
- \(o_1=o_3\)
- \(o_2=o_4\)
- Từ \(o_3=55^{\circ}\), ta có:
- \(o_1=55^{\circ}\)
- Tổng các góc xung quanh điểm \(O\) là \(36 0^{\circ}\): \(o_1+o_2+o_3+o_4=360^{\circ}\)
- Thay giá trị của \(o_1\) và \(o_3\): \(55^{\circ}+o_2+55^{\circ}+o_4=360^{\circ}\) \(110^{\circ}+o_2+o_4=360^{\circ}\) \(o_2+o_4=250^{\circ}\)
- Vì \(o_2=o_4\), ta có: \(2o_2=250^{\circ}\textrm{ }\Longrightarrow\textrm{ o}_2=125^{\circ}\) \(o_4=125^{\circ}\)
- Kết quả:
- \(o_1=55^{\circ}\)
- \(o_2=125^{\circ}\)
- \(o_3=55^{\circ}\)
- \(o_4=125^{\circ}\)
b) Khi \(o_1+o_3=150^{\circ}\)
- Từ \(o_1+o_3=150^{\circ}\) và biết rằng \(o_1=o_3\): \(o_1+o_1=150^{\circ}\textrm{ }\Longrightarrow\textrm{ }2o_1=150^{\circ}\textrm{ }\Longrightarrow\textrm{ o}_1=75^{\circ}\) \(o_3=75^{\circ}\)
- Từ đó, ta có: \(o_2=180^{\circ}-75^{\circ}=105^{\circ}\) \(o_4=105^{\circ}\)
- \(o_2=180^{\circ}-o_1\) (góc phụ)
- \(o_4=o_2\) (góc đối diện)
- Kết quả:
- \(o_1=75^{\circ}\)
- \(o_2=105^{\circ}\)
- \(o_3=75^{\circ}\)
- \(_{O4}=105^{\circ}\)
Tóm tắt kết quả:
- a) \(o_1=55^{\circ},o_2=125^{\circ},o_3=55^{\circ},o_4=125^{\circ}\)
- b) \(o_1=75^{\circ},o_2=105^{\circ},o_3=75^{\circ},o_4=105^{\circ}\)
- THAM KHẢO
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
17 giờ trước (9:22)
Giải:
\(\hat{o_1}\) = \(\hat{O_3}\) = \(55^0\) (hai góc đối đỉnh)
\(\hat{O4}\) + \(\hat{O3}\) = 180\(^0\) (hai góc kề bù)
\(\hat{O_4}\) = 180\(^0\) - \(\hat{O_3}\)
\(\hat{O}_4\) = 180\(^0\) - 55\(^0\) = 125\(^0\)
\(\hat{O_4}\) = \(\hat{O_2}\) = 125\(^0\) (hai góc đối đỉnh)
Mình chỉ chắc 50% thôi nhưng mình nghĩ là cả 4 góc = 90o đó
có 2 đường thẳng a và b cắt nhau tại O
Mà O1 + O3 = O2 + O4
=> O1 + O3 đối đỉnh với O2 + O4
O1 + O3 = 90 ĐỘ và O2 + O4 = 90 ĐỘ