Tính diện tích hình bình hành ABCD biết cạnh AB = 5, AD = 8, góc D = 60°
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
28 tháng 10 2018
Kẻ DH ^ AB tại H
⇒ A H = A D 2 = 4 c m
Áp dụng định lý Pytago trong D vuông ADH Þ DH = 4 3 cm.
ÞSABCD = DH.AB = 120cm2
CM
6 tháng 1 2019
*Khi quay hình bình hành ABCD một vòng quanh cạnh AB thì cạnh AD và BC vạch nên hai hình nón bằng nhau có đường sinh AD = BC = x, cạnh CD vạch nên hình trụ có bán kính đáy bằng bán kính hình nón
Trong tam giác AHD,ta có:
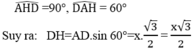
Diện tích toàn phần của hình tạo thành bằng tổng diện tích xung quanh của hai hình nón và diện tích xung quanh của hình trụ
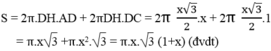
*Khi quay hình bình hành ABCD một vòng quanh AD thì cạnh AB và DC vạch nên hai hình nón bằng nhau có đường sinh AB = DC = 1, cạnh BC vạch nên hình trụ có bán kính đáy bằng bán kính đáy của hình nón
Ta có:
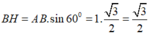
Diện tích toàn phần của hình tạo thành bằng tổng diện tích xung quanh của hai hình nón và diện tích xung quanh của hình trụ
CM
13 tháng 2 2017
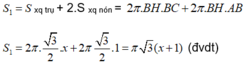
Vì hình ABCD là hình bình hành nên cạnh AD = BC = 3cm. Vì hình BMNC là hình thoi nên có các cạnh bằng nhau, do đó ta có :
BC = BM = MN = 3 cm
Chiều cao tương ứng cạnh DC của hình bình hành ABCD là :
8 : 4 = 2 (cm)
Chiều cao tương ứng cạnh DC cũng là chiều cao tương ứng cạnh NC do đó diện tích hình thoi BMNC là :
3 x 2 = 6 (cm2)
Đáp số : 6 cm2
VM
17 tháng 3 2022
Vì hình ABCD là hình bình hành nên cạnh AD = BC = 3cm. Vì hình BMNC là hình thoi nên có các cạnh bằng nhau, do đó ta có :
BC = BM = MN = 3 cm
Chiều cao tương ứng cạnh DC của hình bình hành ABCD là :
8 : 4 = 2 (cm)
Chiều cao tương ứng cạnh DC cũng là chiều cao tương ứng cạnh NC do đó diện tích hình thoi BMNC là :
3 x 2 = 6 (cm2) Đáp số:6 cm2
1/2 chiều cao hạ từ đỉnh D vuông góc với cạnh AD?
16 tháng 8
ABCD là hình bình hành
=>AB=CD
=>CD=6(cm)
Diện tích tam giác ADC là:
\(S_{ADC}=\frac12\cdot DA\cdot DC\cdot\sin ADC=\frac12\cdot4\cdot6\cdot\sin60=2\cdot6\cdot\frac{\sqrt3}{2}=6\sqrt3\left(\operatorname{cm}^2\right)\)
ABCD là hình bình hành
=>\(S_{ABCD}=2\cdot S_{ADC}=2\cdot6\sqrt3=12\sqrt3\left(\operatorname{cm}^2\right)\)
Ta có: \(\hat{KAB}+\hat{BAD}=180^0\) (hai góc kề bù)
\(\hat{BAD}+\hat{ADC}=180^0\) (ABCD là hình bình hành)
Do đó: \(\hat{KAB}=\hat{ADC}=60^0\)
Xét ΔKAB vuông tại K có \(\sin KAB=\frac{KB}{AB}\)
=>\(\frac{KB}{6}=\sin60=\frac{\sqrt3}{2}\)
=>\(KB=6\cdot\frac{\sqrt3}{2}=3\sqrt3\left(\operatorname{cm}\right)\)
ΔKAB vuông tại K
=>\(KA^2+KB^2=AB^2\)
=>\(KA^2=6^2-\left(3\sqrt3\right)^2=36-27=9=3^2\)
=>KA=3(cm)
Diện tích tam giác KAB là:
\(S_{KAB}=\frac12\cdot KA\cdot KB=\frac12\cdot3\cdot3\sqrt3=\frac{9\sqrt3}{2}\left(\operatorname{cm}^2\right)\)
Ta có: BC//AD
=>\(\hat{HCB}=\hat{ADC}\) (hai góc đồng vị)
=>\(\hat{HCB}=60^0\)
Xét ΔHBC vuông tại H có \(\sin HCB=\frac{HB}{BC}\)
=>\(\frac{HB}{4}=\sin60=\frac{\sqrt3}{2}\)
=>\(HB=4\cdot\frac{\sqrt3}{2}=2\sqrt3\left(\operatorname{cm}\right)\)
ΔBHC vuông tại H
=>\(HB^2+HC^2=BC^2\)
=>\(HC^2=4^2-\left(2\sqrt3\right)^2=16-12=4=2^2\)
=>HC=2(cm)
ΔBHC vuông tại H
=>\(S_{HBC}=\frac12\cdot HB\cdot HC=\frac12\cdot2\cdot2\sqrt3=2\sqrt3\left(\operatorname{cm}^2\right)\)
Diện tích tứ giác KBHD là:
\(S_{KBHD}=S_{ABCD}+S_{BAK}+S_{BCH}\)
\(=12\sqrt3+\frac{9\sqrt3}{2}+2\sqrt3=14\sqrt3+4,5\sqrt3=18,5\sqrt3\left(\operatorname{cm}^2\right)\)
23 tháng 3 2022
Vì hình ABCD là hình bình hành nên cạnh AD = BC = 3cm. Vì hình BMNC là hình thoi nên có các cạnh bằng nhau, do đó ta có: BC = BM = MN = 3 cm Chiều cao tương ứng cạnh DC của hình bình hành ABCD là: 8 : 4 = 2 (cm) Chiều cao tương ứng cạnh DC cũng là chiều cao tương ứng cạnh NC do đó diện tích hình thoi BMNC là : 3 x 2 = 6 (cm2 ) Đáp số: 6 cm2
\(\widehat{A}=180^o-\widehat{D}=180^o-60^o=120^o\)
\(S_{ABD}=\dfrac{1}{2}.AB.AD.sin120^o=10\sqrt{3}\left(đvdt\right)\)
\(\Rightarrow S_{ABCD}=2S_{ABD}=20\sqrt{3}\left(đvdt\right)\)