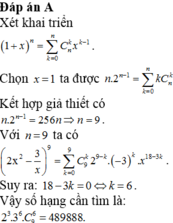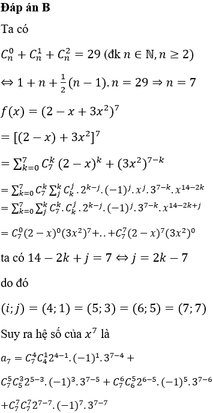Cho khai triển: biết ba hệ số đầu tiên lập thành cấp số cộng. Tìm các số hạng của khai triển nhận giá trị hữu tỷ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án D
Ta có 2 x 2 + 1 x n = ∑ k = 0 n C n k .2 n − k . 1 x k = ∑ k = 0 n C n k . 2 n − k x 2 n − 3 k
Cho 2 n − 3 k = 3 ⇒ C n k .2 n − k = 2 6 . C n 9 .
Giải hệ 2 n − 3 k = 3 C n k .2 n − k = 2 6 . C n 9
Hệ này tương đối khó giải, thử 4 đáp án ta được ⇔ n = 15 k = 9

Ta có:
\(2A_n^2=C_{n-1}^2+C_{n-1}^3\) \(\left(n\ge4\right)\)
\(\Rightarrow2\cdot\dfrac{n!}{\left(n-2\right)!}=\dfrac{\left(n-1\right)!}{2!\left(n-1-2\right)!}+\dfrac{\left(n-1\right)!}{3!\left(n-1-3\right)!}\)
\(\Rightarrow2\cdot n\left(n-1\right)=\dfrac{\left(n-1\right)\left(n-2\right)}{4}+\dfrac{\left(n-1\right)\left(n-2\right)\left(n-3\right)}{6}\)
\(\Rightarrow2n=\dfrac{n-2}{4}+\dfrac{\left(n-2\right)\left(n-3\right)}{6}\)
\(\Rightarrow n=14\) hoặc \(n=0\left(loại\right)\)
Với n=14 ta có khai triển:
\(\left(x^2-\dfrac{1}{x^2}\right)^{14}=\sum\limits^{14}_{k=0}\cdot C_{14}^k\cdot\left(x^2\right)^{14-k}\cdot\left(\dfrac{1}{x^2}\right)^k\)
\(=C_{14}^k\cdot x^{28-4k}\)
Số hạng không chứa x: \(\Rightarrow28-4k=0\Rightarrow k=7\)
Vậy số hạng không chứa x trong khai triển là:
\(C_{14}^7\cdot x^{28-4\cdot7}=C_{14}^7=3432\)

1. Tổng các hệ số của đa thức là: 12004.22005=22005
2.Cần chứng minh x4+x3+x2+x+1=0 vô nghiệm.
Nhận thấy x = 1 không là nghiệm của phương trình .
Nhân cả hai vế của pt cho (x−1)≠0 được :
(x−1)(x4+x3+x2+x+1)=0⇔x5−1=0⇔x=1(vô lí)
Vậy pt trên vô nghiệm.
1. Tổng các hệ số của đa thức là:
12014 . 22015 = 22015
2 . Cần chứng minh.
\(x4 + x3 + x2 + x + 1 = 0\)
Vô nghiệm.
Ta nhận thấy \(x + 1 \) không là nghiệm của phương trình.
Nhân cả hai vế của phương trình cho:
\(( x - 1 ) \) \(\ne\) \(0\) được :
\(( x-1). (x4+x3+x2+x+1)=0\)
\(\Leftrightarrow\)\(5x-1=0\) \(\Leftrightarrow\) \(x = 1\)
Vô lí.
Vậy phương trình trên vô nghiệm.

Câu 2 đề thiếu rồi kìa. Cái cuối cùng là tổ hợp chập bao nhiêu của 2n + 1 thế???
1/ Vì M thuộc \(d_3\) nên ta có tọa độ của M là: \(M\left(2a;a\right)\)
Khoản cách từ M đến \(d_1\) là:
\(d\left(M,d_1\right)=\dfrac{\left|2a+a+3\right|}{\sqrt{1^2+1^2}}=\dfrac{\left|3a+3\right|}{\sqrt{2}}\)
Khoản cách từ M đến \(d_2\) là:
\(d\left(M,d_2\right)=\dfrac{\left|2a-a-4\right|}{\sqrt{1^2+1^2}}=\dfrac{\left|a-4\right|}{\sqrt{2}}\)
Theo đề bài ta có:
\(\dfrac{\left|3a+3\right|}{\sqrt{2}}=2.\dfrac{\left|a-4\right|}{\sqrt{2}}\)
\(\Leftrightarrow\left|3a+3\right|=2.\left|a-4\right|\)
\(\Leftrightarrow a^2+10a-11=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a=1\\a=-11\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}M\left(2;1\right)\\M\left(-22;-11\right)\end{matrix}\right.\)

Câu hỏi của Thi Bùi - Toán lớp 7 - Học toán với OnlineMath
Bạn tham khảo link trên nhé!
 thành một đa thức có {\displaystyle n+1}
thành một đa thức có {\displaystyle n+1} số hạng:
số hạng:

 (1) với mọi số tự nhiên n.
(1) với mọi số tự nhiên n. và {\displaystyle \sum _{k=0}^{n}C_{n}^{k}x^{k+1}=\sum _{k=1}^{n}C_{n}^{k-1}x^{k}+x^{n+1}}
và {\displaystyle \sum _{k=0}^{n}C_{n}^{k}x^{k+1}=\sum _{k=1}^{n}C_{n}^{k-1}x^{k}+x^{n+1}}

 và do đó {\displaystyle (a+b)^{n}=a^{n}(1+{\frac {b}{a}})^{n}=a^{n}\sum _{k=0}^{n}C_{n}^{k}{\frac {b^{k}}{a^{k}}}=\sum _{k=0}^{n}C_{n}^{k}a^{n-k}b^{k}}
và do đó {\displaystyle (a+b)^{n}=a^{n}(1+{\frac {b}{a}})^{n}=a^{n}\sum _{k=0}^{n}C_{n}^{k}{\frac {b^{k}}{a^{k}}}=\sum _{k=0}^{n}C_{n}^{k}a^{n-k}b^{k}}

 :
:
^{4}&=x^{4}+4x^{3}y+6x^{2}y^{2}+4xy^{3}+y^{4},\\[8pt](x+y)^{5}&=x^{5}+5x^{4}y+10x^{3}y^{2}+10x^{2}y^{3}+5xy^{4}+y^{5},\\[8pt](x+y)^{6}&=x^{6}+6x^{5}y+15x^{4}y^{2}+20x^{3}y^{3}+15x^{2}y^{4}+6xy^{5}+y^{6},\\[8pt](x+y)^{7}&=x^{7}+7x^{6}y+21x^{5}y^{2}+35x^{4}y^{3}+35x^{3}y^{4}+21x^{2}y^{5}+7xy^{6}+y^{7}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e30228a99653e6b9a65ae6640a3b7f85e2fdf144)
 giảm dần cho tới khi đạt đến 0 ({\displaystyle x^{0}=1}
giảm dần cho tới khi đạt đến 0 ({\displaystyle x^{0}=1} ), giá trị bắt đầu là {\displaystyle n}
), giá trị bắt đầu là {\displaystyle n} .)
.) tăng lên bắt đầu từ 0 ({\displaystyle y^{0}=1}
tăng lên bắt đầu từ 0 ({\displaystyle y^{0}=1} ) cho tới khi đạt đến {\displaystyle n}
) cho tới khi đạt đến {\displaystyle n} .
.

 là một số thực và {\displaystyle z}
là một số thực và {\displaystyle z} là một số phức có module nhỏ hơn 1 thì:
là một số phức có module nhỏ hơn 1 thì: