Cho (Cm) là đồ thị của hàm số y = x 3 + 3 m x + 1 (với m ∈ ( - ∞ ; 0 ) là tham số thực). Gọi d là đường thẳng đi qua hai điểm cực trị của (Cm). Tìm số các giá trị của m để đường thẳng d cắt đường tròn tâm I(1;0) bán kính R=3 tại hai điểm phân biệt A, Bsao cho diện tích tam giác IAB đạt giá trị lớn nhất.
A.3
B.0
C.1
D.2

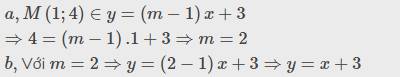
Chọn C
Vì nên phương trình
nên phương trình 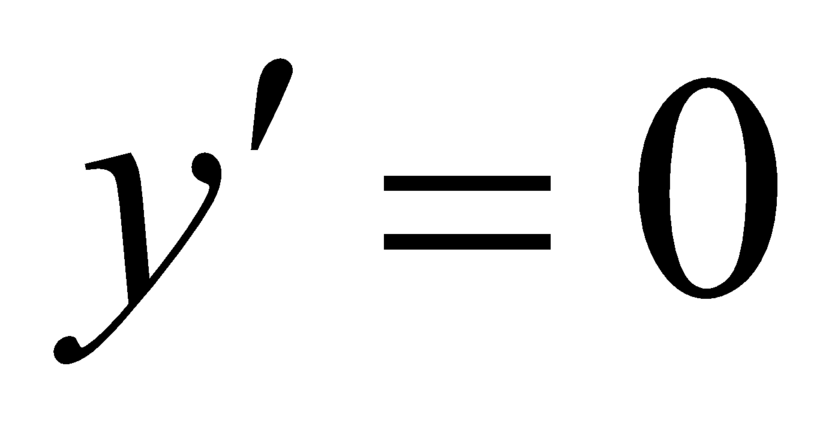 có 2 nghiệm phân biệt.
có 2 nghiệm phân biệt.
Do đó hàm số có hai điểm cực trị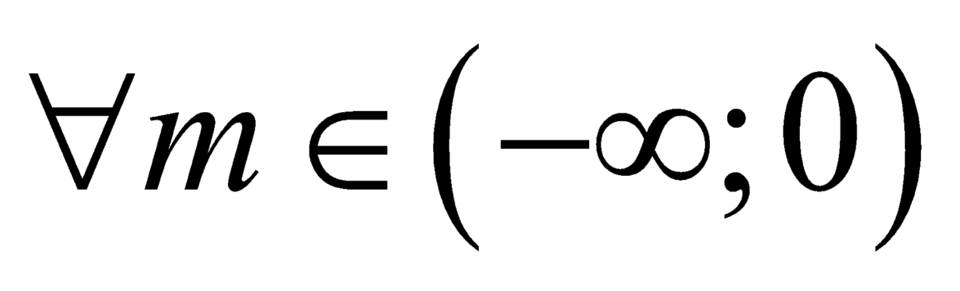 .
.
Giả sử hàm số có hai điểm cực trị lần lượt là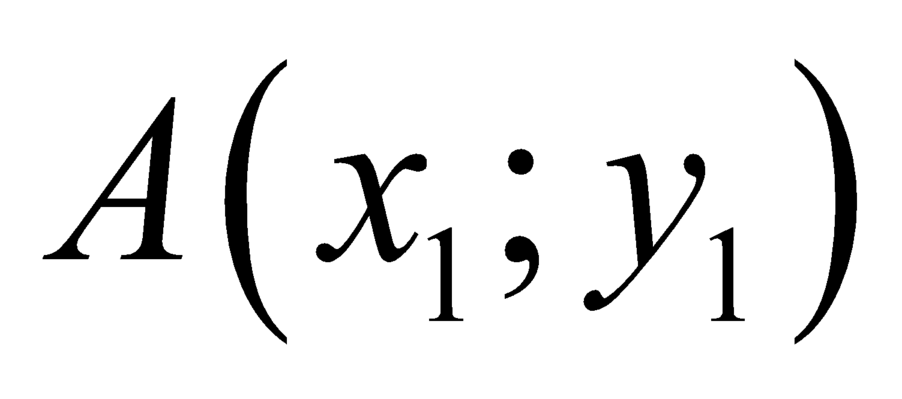 và
và 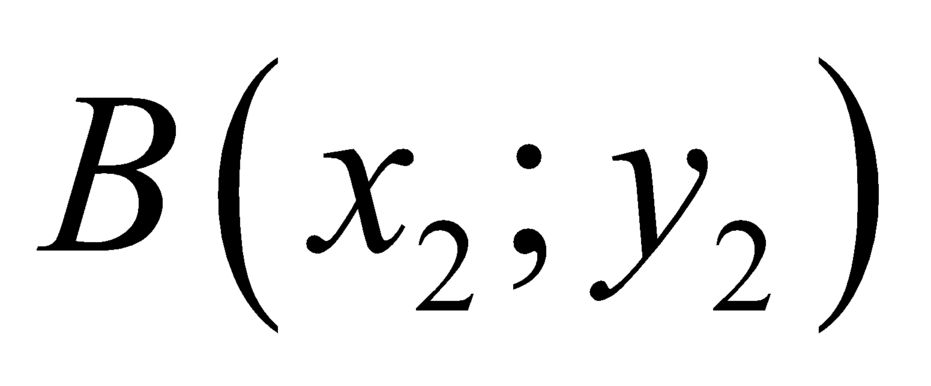 , với
, với 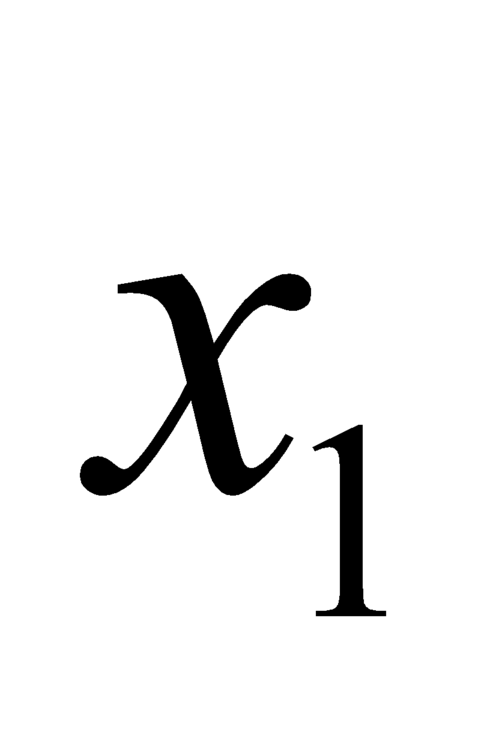 ,
, 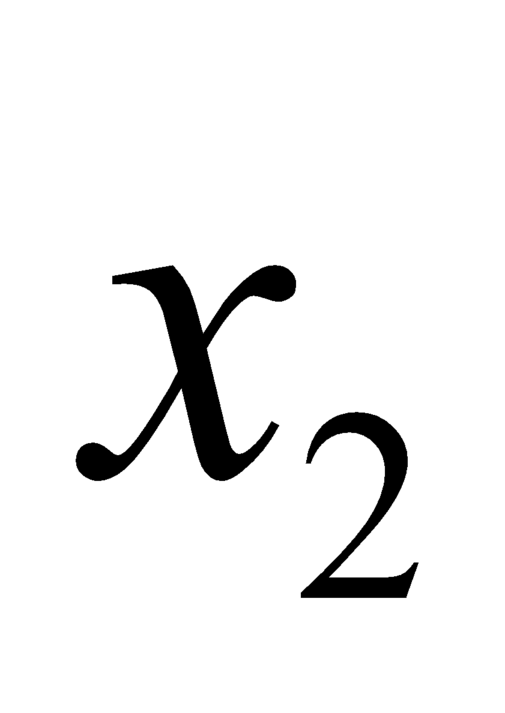 là nghiệm của phương trình
là nghiệm của phương trình 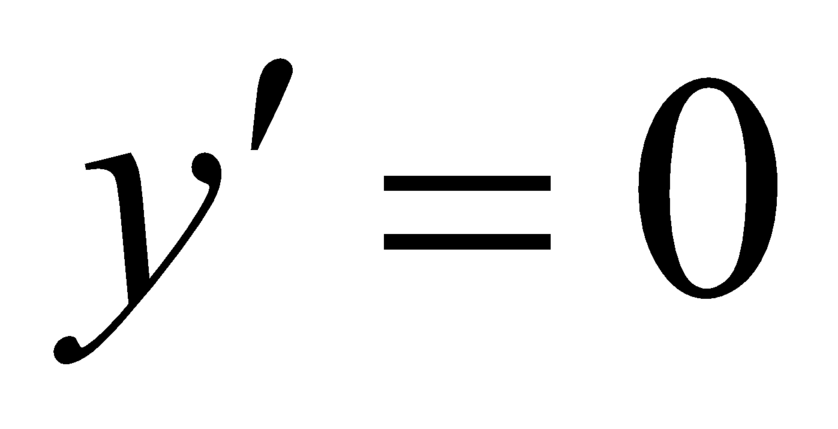 .
.
Thực hiện phép chia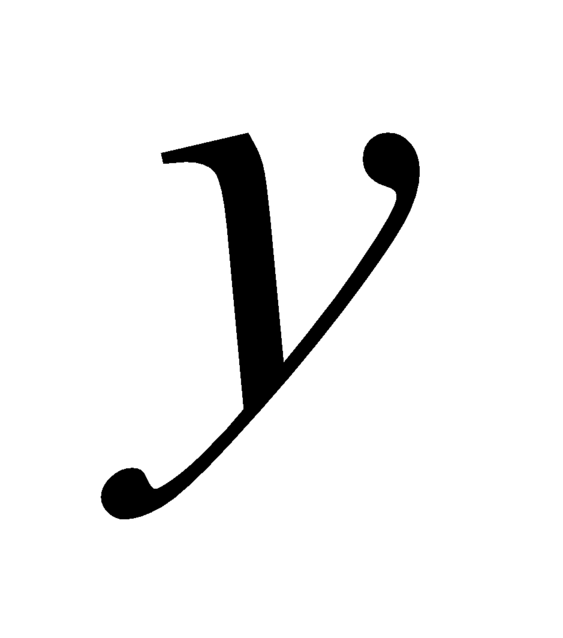 cho
cho  ta được :
ta được : 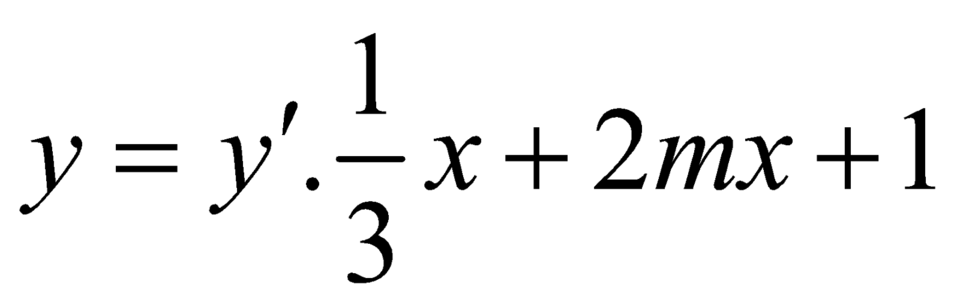 .
.
Khi đó ta có: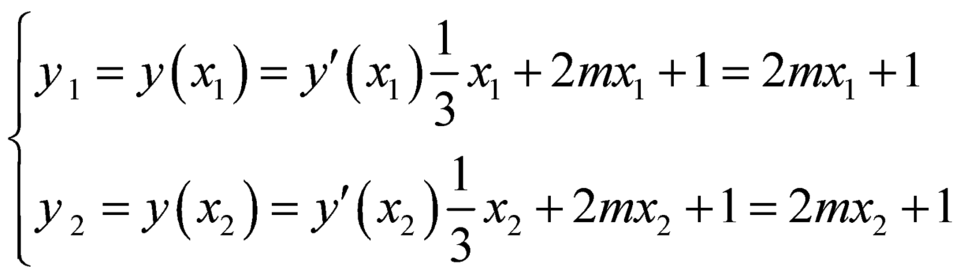 .
.
Ta thấy, toạ độ hai điểm và
và  thoả mãn phương trình
thoả mãn phương trình 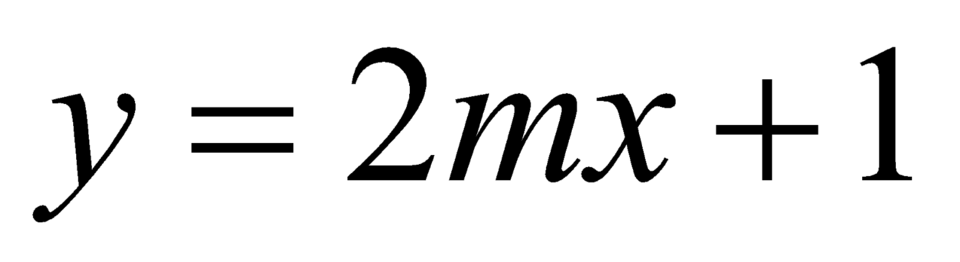 .
.
Do đó, phương trình đường thẳng qua hai điểm cực trị là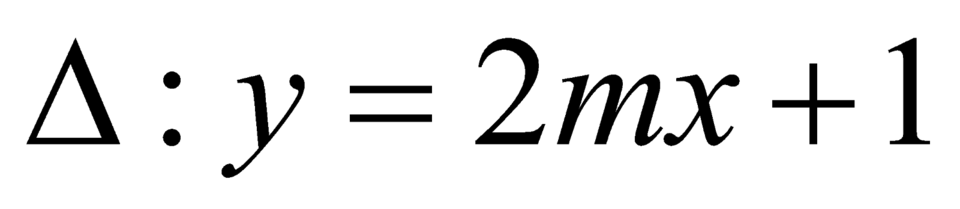 .
.
Ta thấy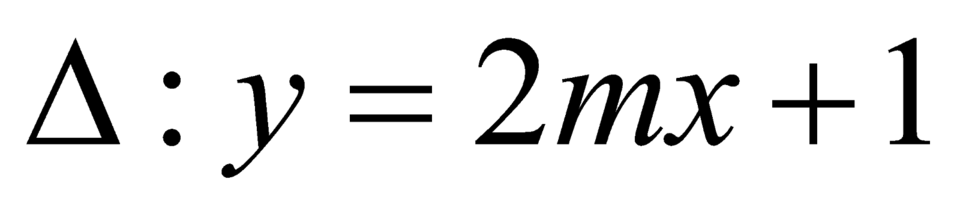 luôn qua
luôn qua 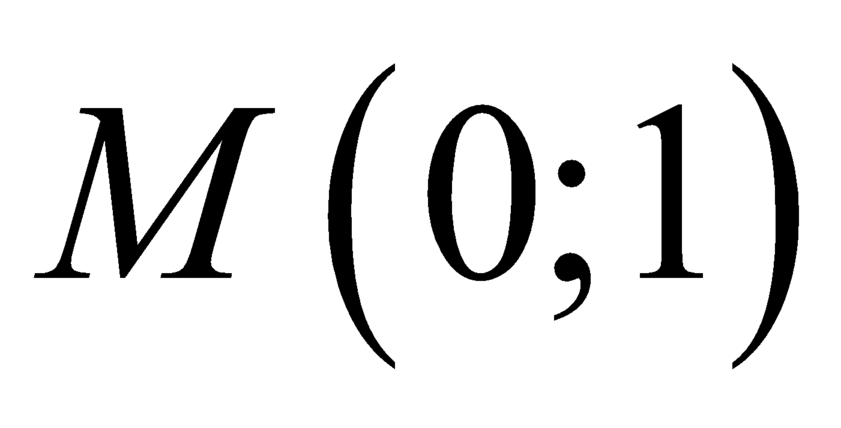 .
.
Đặt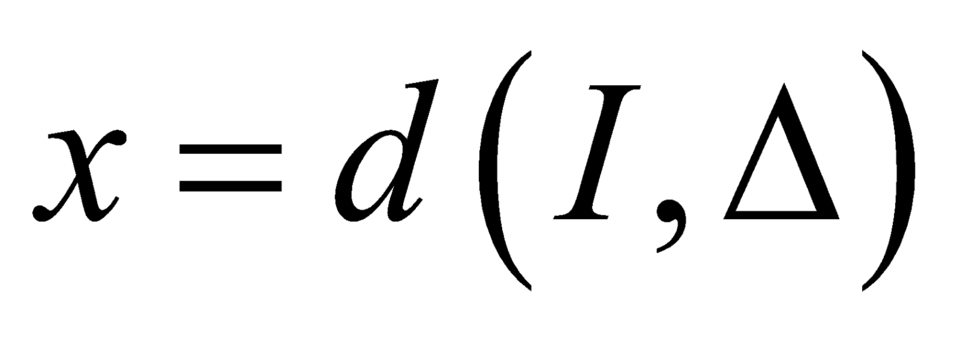
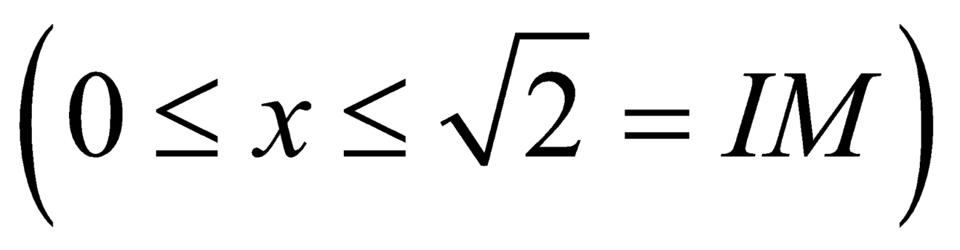 .
.
Xét hàm số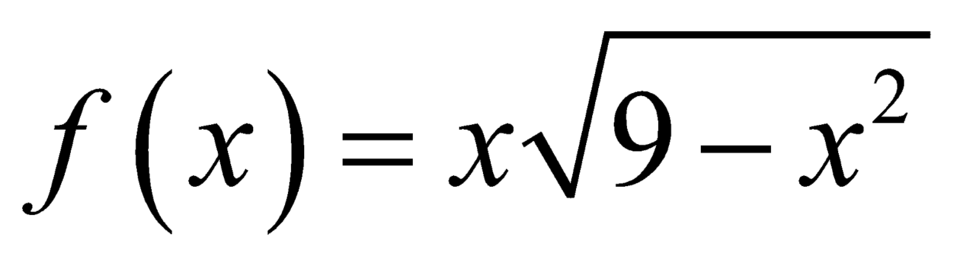 ,
, 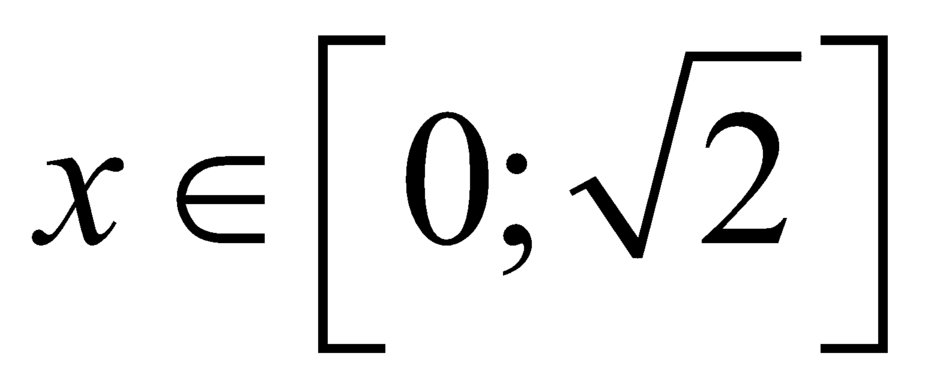 .
.
Suy ra hàm số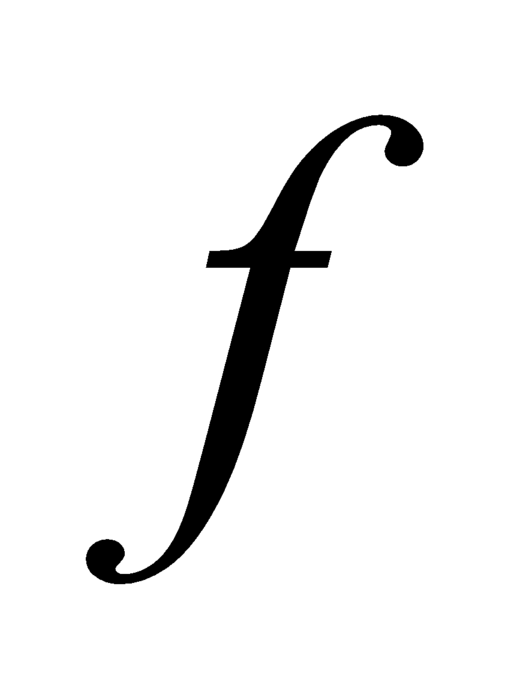 liên tục và đồng biến trên
liên tục và đồng biến trên 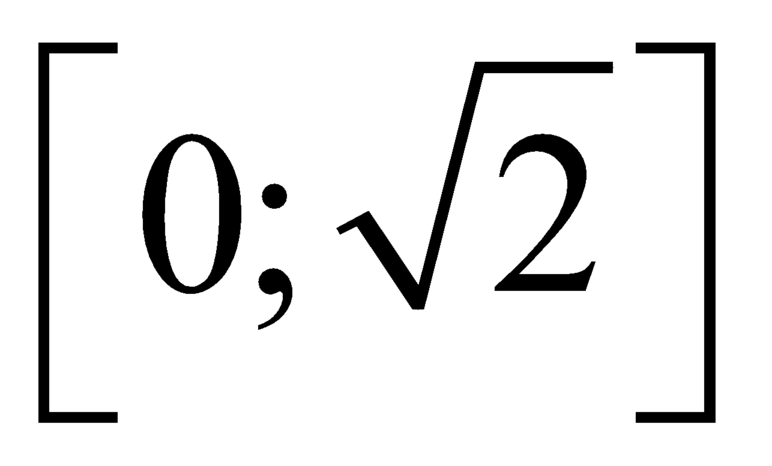 .
.
Do đó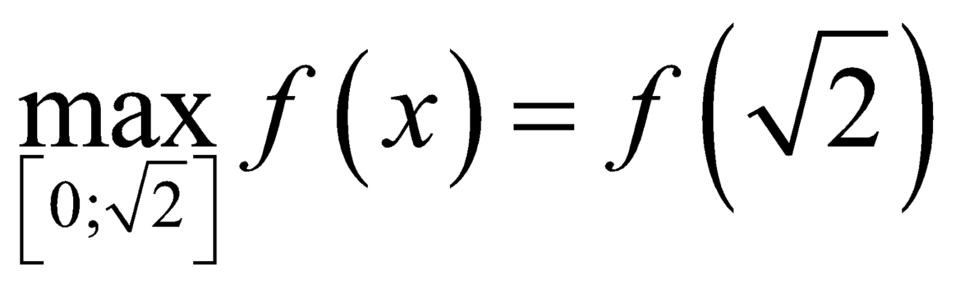 .
.
Vậy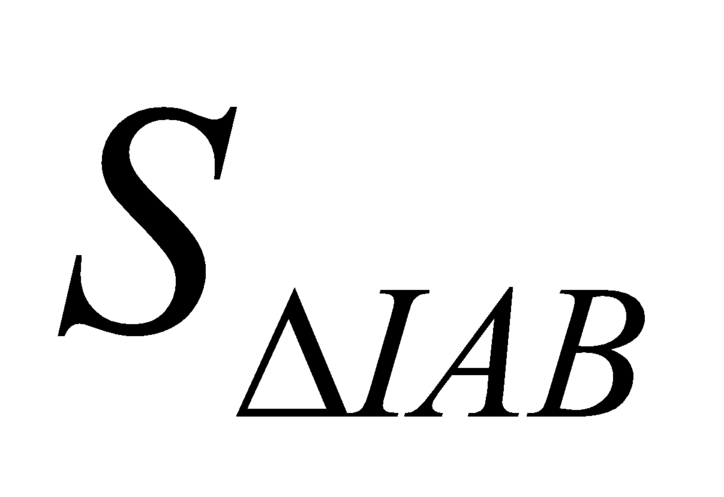 đạt giá trị lớn nhất
đạt giá trị lớn nhất 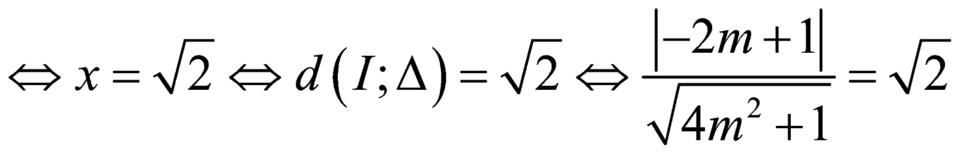
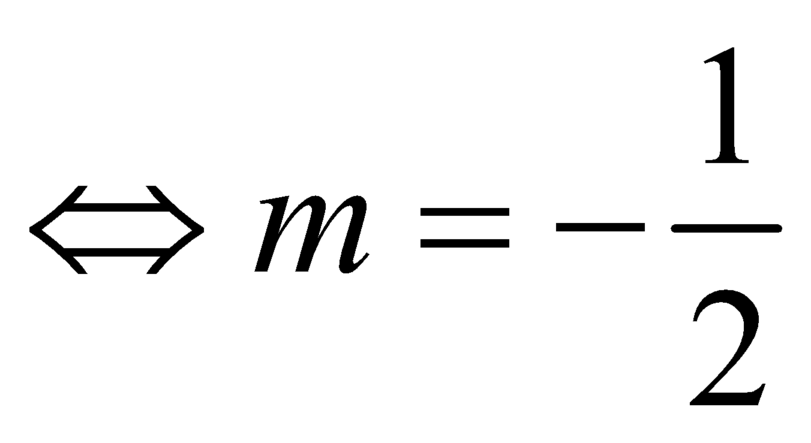 .
.