Xét tính liên tục của hàm số sau tại điểm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
\(\lim\limits_{x\rightarrow0}\dfrac{\sqrt{x+2}-\sqrt{2-x}}{x}=\lim\limits_{x\rightarrow0}\dfrac{2x}{x\left(\sqrt{x+2}+\sqrt{2-x}\right)}=\lim\limits_{x\rightarrow0}\dfrac{2}{\sqrt{x+2}+\sqrt{2-x}}=\dfrac{2}{2\sqrt{2}}=\dfrac{\sqrt{2}}{2}\)
Vậy cần bổ sung \(f\left(0\right)=\dfrac{\sqrt{2}}{2}\) để hàm liên tục tại \(x=0\)
2.
a. \(f\left(0\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^-}\left(x+\dfrac{3}{2}\right)=\dfrac{3}{2}\)
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt{x+1}-1}{\sqrt[3]{1+x}-1}=\lim\limits_{x\rightarrow0^+}\dfrac{x\left(\sqrt[3]{\left(x+1\right)^2}+\sqrt[3]{x+1}+1\right)}{x\left(\sqrt[]{x+1}+1\right)}\)
\(=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt[3]{\left(x+1\right)^2}+\sqrt[3]{x+1}+1}{\sqrt[]{x+1}+1}=\dfrac{3}{2}\)
\(\Rightarrow f\left(0\right)=\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)\) nên hàm liên tục tại \(x=0\)
2b.
\(\lim\limits_{x\rightarrow1^-}f\left(x\right)=\lim\limits_{x\rightarrow1^-}\dfrac{x^3-x^2+2x-2}{x-1}=\lim\limits_{x\rightarrow1^-}\dfrac{x^2\left(x-1\right)+2\left(x-1\right)}{x-1}\)
\(=\lim\limits_{x\rightarrow1^-}\dfrac{\left(x^2+2\right)\left(x-1\right)}{x-1}=\lim\limits_{x\rightarrow1^-}\left(x^2+2\right)=3\)
\(\lim\limits_{x\rightarrow1^+}f\left(x\right)=f\left(1\right)=\lim\limits_{x\rightarrow1^+}\left(3x+a\right)=a+3\)
- Nếu \(a=0\Rightarrow f\left(1\right)=\lim\limits_{x\rightarrow1^-}f\left(x\right)=\lim\limits_{x\rightarrow1^+}f\left(x\right)\) hàm liên tục tại \(x=1\)
- Nếu \(a\ne0\Rightarrow\lim\limits_{x\rightarrow1^-}f\left(x\right)\ne\lim\limits_{x\rightarrow1^+}f\left(x\right)\Rightarrow\) hàm không liên tục tại \(x=1\)

Hàm số \(f\left( x \right) = 2{x^3} + x + 1\) xác định trên \(\mathbb{R}\).
Ta có: \(\begin{array}{l}\mathop {\lim }\limits_{x \to 2} f\left( x \right) = \mathop {\lim }\limits_{x \to 2} \left( {2{x^3} + x + 1} \right) = {2.2^3} + 2 + 1 = 17\\f\left( 2 \right) = {2.2^3} + 2 + 1 = 17\\ \Rightarrow \mathop {\lim }\limits_{x \to 2} f\left( x \right) = f\left( 2 \right)\end{array}\)
Do đó hàm số liên tục tại x = 2.

Đáp án A
(1) Nếu hàm số f(x) có đạo hàm tại điểm x = x 0 thì f(x) liên tục tại điểm đó. Đây là mệnh đề đúng.
(2) Nếu hàm số f (x) liên tục tại điểm x = x 0 thì f(x) có đạo hàm tại điểm đó.
Phản ví dụ
Lấy hàm f ( x ) = x ta có D= R nên hàm số f(x) liên tục trên R.
Nhưng ta có l i m x → 0 + f ( x ) - f ( 0 ) x - 0 = l i m x → 0 + x - 0 x - 0 = l i m x → 0 + x - 0 x - 0 = 1 l i m x → 0 - f ( x ) - f ( 0 ) x - 0 = l i m x → 0 - x - 0 x - 0 = l i m x → 0 - - x - 0 x - 0 = - 1
Nên hàm số không có đạo hàm tại x = 0.
Vậy mệnh đề (2) là mệnh đề sai.
(3) Nếu f(x) gián đoạn tại x = x 0 thì chắc chắn f(x) không có đạo hàm tại điểm đó.
Vì (1) là mệnh đề đúng nên ta có f(x) không liên tục tại x = x 0 thì f(x) không có đạo hàm tại điểm đó.
Vậy (3) là mệnh đề đúng.

+) (1) Nếu hàm số f(x) có đạo hàm tại điểm Xét ba mệnh đề sau:
(1) Nếu hàm số f(x) có đạo hàm tại điểm x = x 0 thì f(x) liên tục tại điểm đó.
(2) Nếu hàm số f(x) liên tục tại điểm x = x 0 thì f(x) có đạo hàm tại điểm đó.
- Trong ba câu trên: thì f(x) liên tục tại điểm đó. Đây là mệnh đề đúng.
+) (2) Nếu hàm số f(x) liên tục tại điểm x = x 0 thì f(x) có đạo hàm tại điểm đó.Đây là mệnh đề sai.
Phản ví dụ:
- Lấy hàm f(x) = |x| ta có D = R nên hàm số f(x) liên tục trên R
- Nhưng ta có
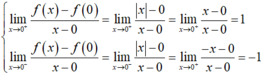
- Nên hàm số không có đạo hàm tại x = 0.
- Vậy mệnh đề (2) là mệnh đề sai.
+) (3) Nếu f(x) gián đoạn tại x = x 0 thì chắc chắn f(x) không có đạo hàm tại điểm đó.
- Vậy (3) là mệnh đề đúng.Vì (1) là mệnh đề đúng nên ta có f(x) không liên tục tại x = x 0 thì f(x) không có đạo hàm tại điểm đó.
- Vậy (3) là mệnh đề đúng.
Chọn A.

+) (1) Nếu hàm số f(x) có đạo hàm tại điểm Xét ba mệnh đề sau:
(1) Nếu hàm số f(x) có đạo hàm tại điểm x = x 0 thì f(x) liên tục tại điểm đó.
(2) Nếu hàm số f(x) liên tục tại điểm x = x 0 thì f(x) có đạo hàm tại điểm đó.
- Trong ba câu trên: thì f(x) liên tục tại điểm đó. Đây là mệnh đề đúng.
+) (2) Nếu hàm số f(x) liên tục tại điểm x = x 0 thì f(x) có đạo hàm tại điểm đó.Đây là mệnh đề sai.
Phản ví dụ:
- Lấy hàm f(x) = |x| ta có D = R nên hàm số f(x) liên tục trên R
- Nhưng ta có
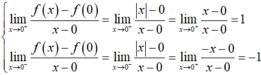
- Nên hàm số không có đạo hàm tại x = 0.
- Vậy mệnh đề (2) là mệnh đề sai.
+) (3) Nếu f(x) gián đoạn tại x = x 0 thì chắc chắn f(x) không có đạo hàm tại điểm đó.
- Vậy (3) là mệnh đề đúng.Vì (1) là mệnh đề đúng nên ta có f(x) không liên tục tại x = x 0 thì f(x) không có đạo hàm tại điểm đó.
- Vậy (3) là mệnh đề đúng.
Chọn A.

(1) Nếu hàm số f(x) có đạo hàm tại điểm x = x 0 thì f(x) liên tục tại điểm đó. Đây là mệnh đề đúng.
(2) Nếu hàm số f(x) liên tục tại điểm x = x 0 thì f(x) có đạo hàm tại điểm đó. Đây là mệnh đề sai.
+)Với mọi
x
0
≠ 0 thì 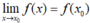
+)Lại có:
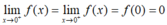
→ Nên hàm số f(x) liên tục trên R.
+) Nhưng ta có:
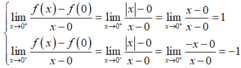
→ Nên hàm số không có đạo hàm tại x = 0.
→ Vậy mệnh đề (2) là mệnh đề sai.
(3) Nếu f(x) gián đoạn tại x = x 0 thì chắc chắn f(x) không có đạo hàm tại điểm đó.
- Vì (1) là mệnh đề đúng nên ta suy ra : Nếu f(x) không liên tục tại x = x 0 thì f(x) không có đạo hàm tại điểm đó.
- Vậy (3) là mệnh đề đúng.
Chọn A.

\(\lim\limits_{x\rightarrow2^+}f\left(x\right)=\lim\limits_{x\rightarrow2^+}-x^2+3x-2=-2^2+3\cdot2-2=0\)
\(\lim\limits_{x\rightarrow2^-}f\left(x\right)=\lim\limits_{x\rightarrow2^-}x+3=2+3=5\)
f(2)=2+3=5
=>\(\lim\limits_{x\rightarrow2^+}f\left(x\right)\ne\lim\limits_{x\rightarrow2^-}f\left(x\right)=f\left(2\right)\)
=>Hàm số gián đoạn tại x=2

Với a = 0, b = 1, hàm số \(f(x) = \left\{ {\begin{array}{*{20}{l}}{2x}&{{\rm{ }}x < 2}\\4&{{\rm{ }}x = 2}\\{ - 3x + 1}&{{\rm{ }}\,x > 2}\end{array}} \right.\)
Ta có:
\(\begin{array}{l}\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ + }} \left( { - 3x + 1} \right) = - 3.2 + 1 = - 5\\\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ - }} \left( {2x} \right) = 2.2 = 4\\ \Rightarrow \mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) \ne \mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right)\end{array}\)
Do đó không tồn tại giới hạn \(\mathop {\lim }\limits_{x \to 2} f\left( x \right)\)
Vậy hàm số không liên tục tại x = 2.
b) Ta có:
\(\begin{array}{l}\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ + }} \left( { - 3x + b} \right) = - 3.2 + b = - 6 + b\\\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ - }} \left( {2x + a} \right) = 2.2 + a = 4 + a\\f\left( 2 \right) = 4\end{array}\)
Để hàm số liên tục tại x = 2 thì \(\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = f\left( 2 \right)\)
\( \Leftrightarrow - 6 + b = 4 + a = 4 \Leftrightarrow \left\{ \begin{array}{l}4 + a = 4\\ - 6 + b = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 0\\b = 10\end{array} \right.\)
Vậy với a = 0 và b = 10 thì hàm số liên tục tại x = 2.
c) Tập xác định của hàm số là: ℝ.
Với x < 2 thì \(f\left( x \right) = 2x + a\) là hàm đa thức nên liên tục.
Với x > 2 thì \(f\left( x \right) = -3x + b\) là hàm đa thức nên liên tục.
Do đó để hàm số liên tục trên ℝ thì hàm số \(f\left( x \right)\) liên tục tại x = 2.
Vậy với a = 0 và b = 10 thỏa mãn điều kiện.
- Tập xác định D = R.
- Ta có: f(2) = 3/2.
- Vì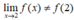 nên hàm số không liên tục tại x = 2.
nên hàm số không liên tục tại x = 2.