Cho khối chóp S.ABC có sao cho Mặt phẳng đi qua hai điểm M, N và song song với SC chia khối chóp thành hai khối đa diện. Tính tỉ số thể tích của hai khối đa diện đó (số bé chia số lớn).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
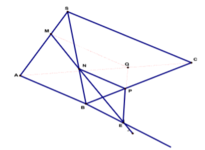
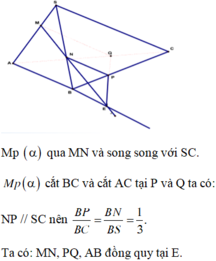
Mp ( α ) qua MN và song song với SC. Mp ( α ) cắt BC và cắt AC tại P và Q ta có:
NP // SC nên ![]() Ta có: MN, PQ, AB đồng quy tại E.
Ta có: MN, PQ, AB đồng quy tại E.
Áp dụng định lí Mennelauyt trong tam giác SAB, ta có:
![]()
![]()
Áp dụng định lí Menelauyt trong tam giác ABC ta có: ![]()
![]()
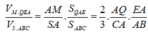
![]()
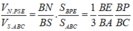
![]()
![]()
![]()
![]()
Vậy 

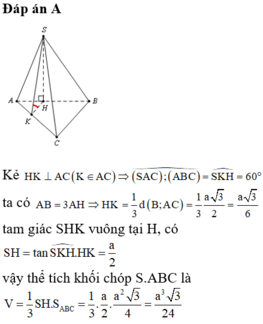
Đáp án A
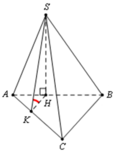
Kẻ H K ⊥ A C K ∈ A C ⇒ S A C ; A B C ^ = S K H ^ = 60 °
ta có A B = 3 A H ⇒ H K = 1 3 d B ; A C = 1 3 a 3 2 = a 3 6
tam giác SHK vuông tại H, có S H = tan S K H ^ . H K = a 2
vậy thể tích khối chóp S.ABC là V = 1 3 S H . S A B C = 1 3 . a 2 . a 2 3 4 = a 3 3 24

Đáp án A
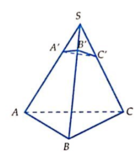
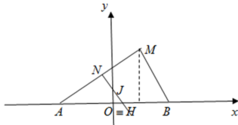
Gọi M là trung điểm của AC. Tam giác ABC vuông tại B, do đó M là tâm đường tròn ngoại tiếp tam giác ABC.
Gọi O là trung điểm của AC, suy ra OM // SA. Mà


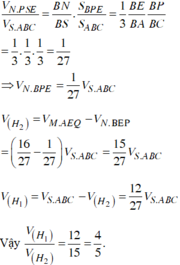

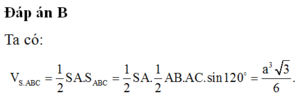





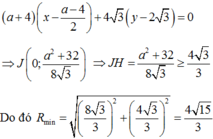

Đáp án B