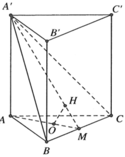
Cho lăng trụ tam giác đều ABC.A’B’C’ cạnh đáy bằng a; chiều cao bằng 2a . Mặt phẳng (P) qua B’ và vuông góc A’C chia lăng trụ thành hai khối. Tính khoảng cách từ điểm A đến (P).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án là C
Gọi G là trọng tâm của tam giác ABC.
Do tam giác ABC đều cạnh a nên 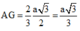
Diện tích tam giác ABC bằng a 3 3 4
Do đỉnh A’ cách đều ba đỉnh A, B, C nên A'G ⊥ (ABC) => A'G là đường cao của khối lăng trụ.
Theo giả thiết, ta có
A
'
A
G
^
=
45
0
=>
∆
A'GA vuông cân. Tù đó suy ra ![]()
Vậy thể tích của khối lăng trụ bằng ![]()
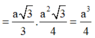

Phương pháp
Tính chiều cao lăng trụ dựa vào định lý Pytago
Tính thẻ tích lăng trụ V = S.h với S là diện tích đáy và h là chiều cao lăng trụ
Cách giải:
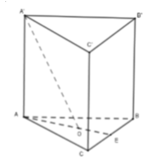
Gọi E là trung điểm của BC.

Chọn A


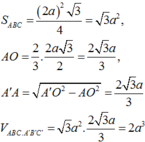


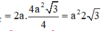

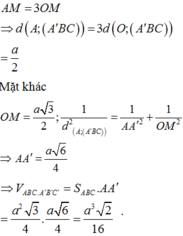

Đáp án đúng : C