Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Để phân số \(\frac{n+3}{n-2}\)có giá trị nguyên
=> n + 3 \(⋮\)n - 2
=> n - 2 + 5 \(⋮\)n - 2
=> ( n - 2 ) + 5 \(⋮\)n - 2
=> 5 \(⋮\)n - 2
=> n - 2 \(\in\)Ư ( 5 ) = { 1 ; 5 }
Với n - 2 = 1 => n = 3
Với n - 2 = 5 => n = 7
Vậy : n \(\in\){ 3 ; 7 }
\(B=\left(n+3\right)^2-\left(n-4\right)^2\)
\(=\left(n+3-n+4\right)\left(n+3+n-4\right)\)
\(=7\left(2n-1\right)\)
Dễ thấy B là số nguyên tố khi
\(2n-1=1\Leftrightarrow n=1\)
Vậy n = 1 thì B là số nguyên tố
Tập hợp các giá trị tự nhiên của n để phân thức (n4-2n3+5)/(n-2) có các giá trị nguyên là bao nhiêu?
\(\left(n^4-2n^3+5\right)=n^3\left(n-2\right)+5\) chia hết cho n -2
=> 5 chia hết cho n -2
n-2 thuộc U(5) = {1;5}
=> n thuộc { 3;7}
Vậy tập hợp có 2 phần tử
Điều kiện xác định của phân thức: n ≠ 2
Ta có:
Vậy để N nguyên thì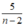
nguyên ⇒ n – 2 là ước của 5;
Ư
(
5
)
=
-
1
;
1
;
-
5
;
5
n - 2= -1 ⇒ n =1;
n – 2 = 1 ⇒ n =3;
n – 2 = -5 ⇒ n = - 3;
n – 2 = 5 ⇒ n = 7;
vì n ∈ N nên n = 1; n = 3; n = 7
Vậy với n ∈ { 1; 3; 7} thì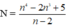
có giá trị là số nguyên