Tính các góc của tứ giác ABCD, biết rằng : Góc A, Góc B, Góc C, Góc D lần lượt bằng 1,2,3,4.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Xét tứ giác ABCD có
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\)(Định lí tổng bốn góc trong một tứ giác)
mà \(\dfrac{\widehat{A}}{1}=\dfrac{\widehat{B}}{2}=\dfrac{\widehat{C}}{3}=\dfrac{\widehat{D}}{4}\)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{\widehat{A}}{1}=\dfrac{\widehat{B}}{2}=\dfrac{\widehat{C}}{3}=\dfrac{\widehat{D}}{4}=\dfrac{\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}}{1+2+3+4}=\dfrac{360^0}{10}=36^0\)
Do đó: \(\widehat{A}=36^0;\widehat{B}=72^0;\widehat{C}=108^0;\widehat{D}=144^0\)
Ta có: \(\widehat{B}+\widehat{C}=180^0\)
mà hai góc này là hai góc trong cùng phía
nên AB//CD(dấu hiệu nhận biết hai đường thẳng song song)
hay ABCD là hình thang

1. Xét tứ giác ABCD ta có :
^A + ^B + ^C + ^D = 3600 ( định lí )
mà 4 góc đó bằng nhau
=> ^A = ^B = ^C = ^D = 3600/4 = 900
2. Xét tứ giác ABCD ta có :
^A + ^B + ^C + ^D = 3600 ( định lí ) (1)
mà ^A , ^B , ^C , ^D lần lượt tỉ lệ với 1 ; 2 ; 4 ; 5
=> \(\frac{\widehat{A}}{1}=\frac{\widehat{B}}{2}=\frac{\widehat{C}}{4}=\frac{\widehat{D}}{5}\)(2)
Từ (1) và (2) => Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{\widehat{A}}{1}=\frac{\widehat{B}}{2}=\frac{\widehat{C}}{4}=\frac{\widehat{D}}{5}=\frac{\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}}{1+2+4+5}=\frac{360^0}{12}=30^0\)
=> ^A = 300
^B = 300.2 = 600
^C = 300.4 = 1200
^D = 300.5 = 1500
Xét tứ giác ABCD có các góc bằng nhau
=> \(\widehat{A}=\widehat{B}=\widehat{C}=\widehat{D}\)
Mà \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\left(dl\right)\)
\(\Leftrightarrow4\widehat{A}=360^o\Leftrightarrow\widehat{A}=\widehat{B}=\widehat{C}=\widehat{D}=90^o\)
Bài 2:
Xét tứ giác ABCD
=> \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\)
Vì các góc tứ giác ABCD lần lượt tỉ lệ với 1:2:4:5
\(\Rightarrow\frac{\widehat{A}}{1}=\frac{\widehat{B}}{2}=\frac{\widehat{C}}{4}=\frac{\widehat{D}}{5}\)VÀ \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\)
Theo tính chất dãy tỉ số bằng nhau
\(\frac{\widehat{A}}{1}=\frac{\widehat{B}}{2}=\frac{\widehat{C}}{4}=\frac{\widehat{D}}{5}=\frac{\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}}{1+2+4+5}=\frac{360^o}{12}=30^o\)
Do đó
\(\frac{\widehat{A}}{1}=30^o\Leftrightarrow\widehat{A}=30^o\)
\(\frac{\widehat{B}}{2}=30^o\Leftrightarrow\widehat{B}=60^o\)
\(\frac{\widehat{C}}{4}=30^o\Leftrightarrow\widehat{C}=120^o\)
\(\frac{\widehat{C}}{5}=30^o\Leftrightarrow\widehat{C}=150^o\)
Vậy.........

Kí hiệu: ∠ : góc
Các góc của tứ giác là ∠A, ∠B, ∠C, ∠D (∠A > 0) tạo thành cấp số cộng:
⇒ ∠B = ∠A + d,
∠C = ∠A + 2d,
∠D = ∠A + 3d.
Theo giả thiết, góc C gấp năm lần góc A nên:
∠C = 5∠A
⇒ ∠A + 2d = 5∠A
⇒ 2d = 4∠A
hay d = 2.∠A
Tổng 4 góc của 1 tứ giác bằng 360º nên ta có:
⇒ ∠A + ∠B + ∠C + ∠D = 360º
⇒ ∠A + ∠A + d + ∠A + 2d + ∠A + 3d = 360º
=> 4∠A +6d = 360º
⇒ 4∠A + 12∠A = 360º ( do d = 2.ºA)
⇒ 16∠A = 360º
⇒ ∠A = 22º30'
⇒ d = 45º.
Vậy ∠A = 22º30' ; ∠B = 67º30'; ∠C = 112º30’; ∠D = 157º30'

a) Ta có: AB = AD (gt) => A thuộc đường trung trực của BD
CB = CD (gt) => C thuộc đường trung trực của BD.
Vậy AC là đường trung trực của BD.
b) Xét ∆ ABC và ∆ADC có AB = AD (gt)
nên ∆ ABC = ∆ADC (c.c.c)
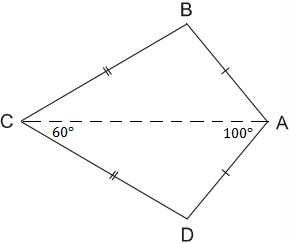
Suy ra: ⇒ˆB=ˆD
Ta có ˆB+ˆD=3600–(100+60)=200
Do đó ˆB=ˆD=1000

Ta có: góc B- góc A=200 <=> Góc B= góc A+200 (1) ; góc C= 3 góc A ( giả thiết) (2) ; góc D- góc C=200 <=> góc D= 3 góc A+200 (theo(2))
Mà : góc A+ góc B+ góc C+ góc D=3600 (*). Thay (1);(2);(3) vào (*), ta được: Góc A+ góc A+200+3 góc A+3 góc A+200=3600
<=> Góc A= 400 => Các góc còn lại
Gọi số đo góc A là x
thì số đo góc B là: x + 20
số đo góc C là: 3x => số đo góc D là: 3x + 20
Ta có: \(x+\left(x+20\right)+3x+\left(3x+20\right)=180\)
\(\Leftrightarrow\)\(8x=140\)
\(\Leftrightarrow\)\(x=17,5\)
Vậy góc A = 17,50
góc B = 17,50 + 200 = 37,50
góc C = 17,5 . 3 = 52,50
góc D = 52,50 + 200 = 72,50

Áp dụng tcdtsbn:
\(\dfrac{\widehat{A}}{1}=\dfrac{\widehat{B}}{2}=\dfrac{\widehat{C}}{3}=\dfrac{\widehat{D}}{4}=\dfrac{\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}}{1+2+3+4}=\dfrac{360^0}{10}=36^0\\ \Rightarrow\left\{{}\begin{matrix}\widehat{A}=36^0\\\widehat{B}=72^0\\\widehat{C}=108^0\\\widehat{D}=144^0\end{matrix}\right.\)
Áp dụng gì thế bạn ơi ;-;