cho hàm số f(f(x)+2y)=4x+4y+3 với mọi số thực x, y. Tìm f(x)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
31 tháng 1 2022
a) Ta có: \(y=f\left(x\right)=4x^2-5\)
\(\Rightarrow\left\{{}\begin{matrix}f\left(3\right)=4.3^2-5=31\\f\left(-\dfrac{1}{2}\right)=4.\left(-\dfrac{1}{2}\right)^2-5=-4\end{matrix}\right.\)
b) Ta có: \(f\left(x\right)=-1\)
\(\Rightarrow4x^2-5=-1\)
\(\Leftrightarrow4x^2=4\)
\(\Leftrightarrow x^2=1\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
Vậy \(x\in\left\{1;-1\right\}\) thì \(f\left(x\right)=-1\)
c) \(\forall x\in R,f\left(x\right)=f\left(-x\right)\Leftrightarrow f\left(-x\right)=4.\left(-x\right)^2-5=4x^2-5=f\left(x\right)\)
Vậy \(\forall x\in R\) thì \(f\left(x\right)=f\left(-x\right)\)
31 tháng 1 2022
\(a.f\left(3\right)=4.3^2-5=31.\\ f\left(\dfrac{-1}{2}\right)=4.\left(\dfrac{-1}{2}\right)^2-5=-4.\)
\(b.f\left(x\right)=-1.\Rightarrow4x^2-5=-1.\\ \Leftrightarrow4x^2=4.\Leftrightarrow x^2=1.\\ \Leftrightarrow x=\pm1.\)
\(c.f\left(x\right)=f\left(-x\right).\\ \Rightarrow4x^2-5=4\left(-x\right)^2-5.\\ \Leftrightarrow4x^2-5=4x^2-5.\)
\(\Leftrightarrow0x=0\) (luôn đúng).
Vậy với mọi x ∈ R thì f (x)= f (-x).
CM
1 tháng 6 2017
Đáp án B
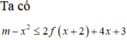
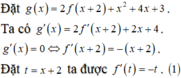
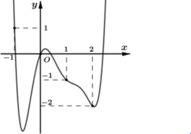
(1) là phương trình hoành độ giao điểm của đồ thị f'(t) và đường thẳng d : y = -t (hình vẽ)
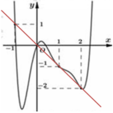
Dựa vào đồ thị của f'(t) và đường thẳng y =-t ta có
NT
0
có 
thì đồng biến trên R.
23 tháng 12 2023
Câu 5:
a: Khi m=3 thì \(f\left(x\right)=\left(2\cdot3+1\right)x-3=7x-3\)
\(f\left(-3\right)=7\cdot\left(-3\right)-3=-21-3=-24\)
\(f\left(0\right)=7\cdot0-3=-3\)
b: Thay x=2 và y=3 vào f(x)=(2m+1)x-3, ta được:
\(2\left(2m+1\right)-3=3\)
=>2(2m+1)=6
=>2m+1=3
=>2m=2
=>m=1
c: Thay m=1 vào hàm số, ta được:
\(y=\left(2\cdot1+1\right)x-3=3x-3\)
*Vẽ đồ thị
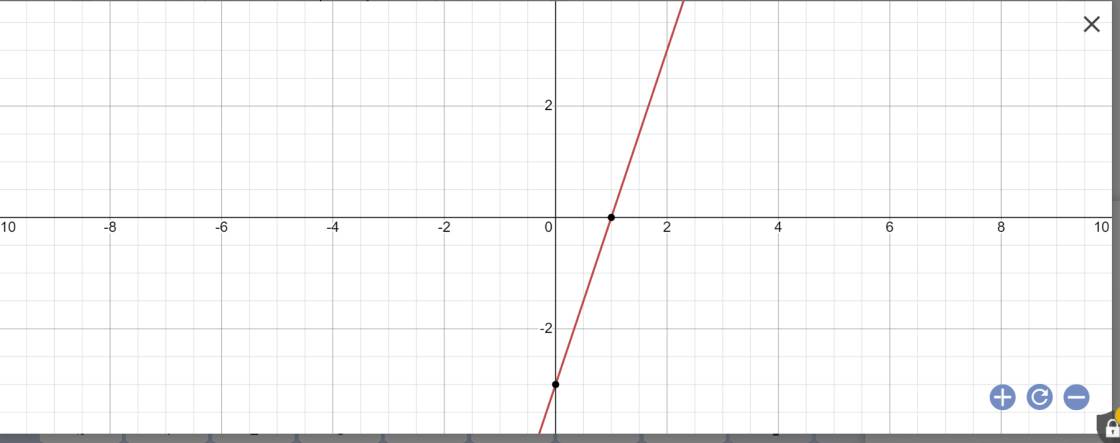
d: Để hàm số y=(2m+1)x-3 là hàm số bậc nhất thì \(2m+1\ne0\)
=>\(2m\ne-1\)
=>\(m\ne-\dfrac{1}{2}\)
e: Để đồ thị hàm số y=(2m+1)x-3 song song với đường thẳng y=5x+1 thì \(\left\{{}\begin{matrix}2m+1=5\\-3\ne1\end{matrix}\right.\)
=>2m+1=5
=>2m=4
=>m=2
G
27 tháng 12 2020
a) Có: y = f(x) = 4x2 - 3
=> f(-2) = 4 . (-2) - 3
= -11
Vậy f(-2) = -11
b) Có: f(x) = 4x2 - 3
Mà f(x) = 1
=> 4x2 - 3 = 1
<=> 4x2 = 4
<=> x2 = 1
<=> x = 1 hoặc x = -1
Vậy x = 1 hoặc x = -1 thì f(x) = 1.
c) Có: f(x) = 4x2 - 3
Mà f(x) = x
=> 4x2 - 3 = x
<=> 4x2 - 3 - x = 0
<=> (4x2 + 3x) - (4x + 3) = 0
<=> x(4x + 3) - (4x+ 3) = 0
<=> (x - 1)(4x + 3) = 0
<=> x - 1 = 0 hoặc 4x + 3 = 0
<=> x = 1 hoặc 4x = -3
<=> x = 1 hoặc x = \(-\frac{3}{4}\)
Vậy x = 1 hoặc x = \(-\frac{3}{4}\) thì f(x) = x.
Linz
28 tháng 12 2020
a, \(f\left(-2\right)=4\left(-2\right)^2-3=16-3=13\)
b, \(f\left(x\right)=1\)hay \(f\left(x\right)=4x^2-3=1\)
\(\Leftrightarrow x^2=1\Leftrightarrow x=\pm1\)
c, \(f\left(x\right)=x\)hay \(4x^2-3=x\)
\(\Leftrightarrow4x^2-3-x=0\Leftrightarrow3x^2+x^2-3-x=0\)
\(\Leftrightarrow3\left(x^2-1\right)+x\left(x-1\right)=0\)
\(\Leftrightarrow3\left(x-1\right)\left(x+1\right)+x\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left[3\left(x+1\right)+x\right]=0\)
\(\Leftrightarrow\left(x-1\right)\left(4x+3\right)=0\Leftrightarrow x=1;-\frac{3}{4}\)
Nhận xét: f(x) là đơn ánh.
Thật vậy, giả sử f(x1)=f(x2) thì: f(f(x1)+2y)=f(f(x2)+2y)
=> 4x1+4y+3=4x2+4y+3<=>x1=x2. Vậy f là đơn ánh
Ta có: f(f(x)+2y)=4x+4y+3=f(f(y)+2x)
Vì f là đơn ánh nên: f(x)+2x=f(y)+2x hay f(x)-2x=f(y)-2y. Với mọi x,y thuộc R
Do đó: f(x)-2x=c, c thuộc R. Thay f(x)=2x+c vào điều kiện ta có c=1
Vậy f(x)=2x+1 (TMĐK)