Cho (𝑂) ∩ (𝑂′) = {𝐴; 𝐷} (𝑂, 𝑂′ thuộc hai nửa mặt phẳng khác nhau bờ AD). Trong (O) vẽ dây CD, trong (O’) vẽ dây DB sao cho CD là tiếp tuyến của (O’); DB là tiếp tuyến của (O).Chứng minh rằng: \(\frac{AC}{AB}=\frac{DC^2}{DB^2}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TH
Trần Hoàng Trung
VIP
3 tháng 9
Bạn ơi, câu hỏi có vẻ thiếu một số thông tin hoặc có nhầm lẫn nhỏ trong phần mô tả (như “trung điểm của \(B C\)” — chưa biết điểm \(C\) ở đâu), nên mình sẽ giả sử và giải bài theo cách thông thường nhất liên quan đến đường tròn, tiếp tuyến, và trục đối xứng nhé!
Giả sử đề bài như sau:
Cho đường tròn \(\left(\right. O ; R \left.\right)\) và một đường thẳng \(x\) cắt đường tròn tại hai điểm phân biệt \(A\) và \(B\). Gọi \(y\) là đường thẳng đi qua trung điểm của đoạn thẳng \(A B\) và vuông góc với \(A B\).
Chứng minh: Đường thẳng \(y\) là trục đối xứng của đường tròn \(\left(\right. O \left.\right)\).
Lời giải:
- Gọi \(M\) là trung điểm của đoạn \(A B\).
- Vì \(A , B\) thuộc đường tròn \(\left(\right. O ; R \left.\right)\), ta có:
\(O A = O B = R\)
- Đường thẳng \(y\) đi qua \(M\) và vuông góc với \(A B\). Đây là đường trung trực của đoạn \(A B\).
- Vì \(O\) nằm trên đường trung trực của \(A B\) (vì \(O A = O B\)) nên \(O\) cũng nằm trên đường thẳng \(y\).
- Đường thẳng \(y\) đi qua tâm \(O\) và vuông góc với \(A B\), nên \(y\) là trục đối xứng của đoạn \(A B\).
- Vì đường tròn là hình tròn tâm \(O\), có tính đối xứng trục qua mọi đường thẳng đi qua \(O\).
- Như vậy, \(y\) là trục đối xứng của đường tròn \(\left(\right. O \left.\right)\).
Kết luận:
- Đường thẳng đi qua trung điểm \(M\) của đoạn \(A B\) và vuông góc với \(A B\) là trục đối xứng của đường tròn \(\left(\right. O ; R \left.\right)\).
3 tháng 9
Sửa đề: Xác định vị trí tương đối của các điểm A,B,C,D với đường tròn (A;4cm)
ABCD là hình vuông
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
O là trung điểm của AC
=>\(AC=2\cdot AO=2\cdot2\sqrt2=4\sqrt2\left(\operatorname{cm}\right)\)
ΔABC vuông tại B
=>\(BA^2+BC^2=AC^2\)
=>\(2\cdot AB^2=AC^2=\left(4\sqrt2\right)^2=32\)
=>\(AB^2=16=4^2\)
=>AB=4(cm)
Vì ABCD là hình vuông
nên AB=AD=4cm
=>D nằm trên (A;4cm) và B cũng nằm trên (A;4cm)
Vì AC>AB
nên C nằm ngoài (A;4cm)
TH
Trần Hoàng Trung
VIP
3 tháng 9
🎯 Đề bài tóm tắt:
- \(A B C D\) là hình vuông
- \(O\) là giao điểm hai đường chéo → O là tâm hình vuông
- \(O A = 2 \sqrt{2} \&\text{nbsp};\text{cm}\)
- Vẽ đường tròn tâm A, bán kính 4 cm → gọi là \(\left(\right. A ; 4 \&\text{nbsp};\text{cm} \left.\right)\)
- Hỏi: Vị trí tương đối của các điểm \(A , B , C , D\) so với đường tròn \(\left(\right. O ; 4 \&\text{nbsp};\text{cm} \left.\right)\)
✳️ Bước 1: Phân tích hình vuông
Vì \(O\) là tâm hình vuông ⇒ các đoạn \(O A = O B = O C = O D\)
- Đề bài cho: \(O A = 2 \sqrt{2} \&\text{nbsp};\text{cm}\)
- Vậy \(O B = O C = O D = 2 \sqrt{2} \&\text{nbsp};\text{cm}\)
✳️ Bước 2: Xét đường tròn \(\left(\right. O ; 4 \&\text{nbsp};\text{cm} \left.\right)\)
- Đây là đường tròn tâm O, bán kính \(R = 4 \&\text{nbsp};\text{cm}\)
- Ta cần xét các điểm \(A , B , C , D\) nằm trên, trong hay ngoài đường tròn này
✅ Bước 3: So sánh các khoảng cách với bán kính 4 cm
Điểm | Khoảng cách đến O | So với bán kính 4 cm | Kết luận vị trí |
|---|---|---|---|
A | \(O A = 2 \sqrt{2} \approx 2.83 \&\text{nbsp};\text{cm}\)OA=22≈2.83 cmOA=22≈2.83 cm | < 4 cm | A nằm trong đường tròn |
B | \(O B = 2 \sqrt{2} \approx 2.83 \&\text{nbsp};\text{cm}\)OB=22≈2.83 cmOB=22≈2.83 cm | < 4 cm | B nằm trong đường tròn |
C | \(O C = 2 \sqrt{2} \approx 2.83 \&\text{nbsp};\text{cm}\)OC=22≈2.83 cmOC=22≈2.83 cm | < 4 cm | C nằm trong đường tròn |
D | \(O D = 2 \sqrt{2} \approx 2.83 \&\text{nbsp};\text{cm}\)OD=22≈2.83 cmOD=22≈2.83 cm | < 4 cm | D nằm trong đường tròn |
✍️ Kết luận cuối cùng:
Vì \(O A = O B = O C = O D = 2 \sqrt{2} < 4\), nên các điểm \(A , B , C , D\) đều nằm bên trong đường tròn \(\left(\right. O ; 4 \&\text{nbsp};\text{cm} \left.\right)\)
✅ Trả lời:
Các điểm \(A , B , C , D\) đều nằm trong đường tròn \(\left(\right. O ; 4 \&\text{nbsp};\text{cm} \left.\right)\)
11 tháng 8
GT l Góc xOy< 180 độ ; OA<OC; OB=OA: OD=OC
KL l a) O là góc chung của tam giác ? và tam giác ?. Tam giác OAD = tam giác OBC
b) Góc ODA = góc OCB; DA=BC
a) O là góc chung của 2 tam giác OAD và OBC.
Xét tam giác OAD và tam giác OBC:
+ Chung góc O
+ OA = OB (gt)
+ OC=OD
==> Tam giác OAD = tam giác OBC ( c.g.c)
Vậy tam giác OAD = tam giác OBC
b) Ta có: Tam giác OAD = tam giác OBC ( cmt)
==> Góc OAD = góc OCB ( 2 góc tương ứng ) ; DA=BC ( 2 cạnh tương ứng )
Vậy góc OAD = góc OCB; DA=BC
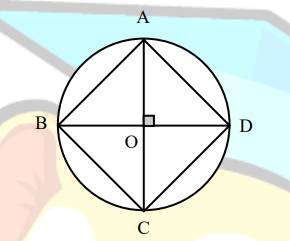
+ \(\left\{{}\begin{matrix}\widehat{ADC}=\widehat{ABD}\left(=\frac{1}{2}sđ\stackrel\frown{AD}của\left(O'\right)\right)\\\widehat{ACD}=\widehat{ADB}\left(=\frac{1}{2}sđ\stackrel\frown{AD}của\left(O\right)\right)\end{matrix}\right.\)
=> ΔABD ∼ ΔADC (g.g)
\(\Rightarrow\frac{AD}{AB}=\frac{AC}{AD}=\frac{CD}{BD}\)
\(\Rightarrow\frac{AD}{AB}\cdot\frac{AC}{AD}=\frac{CD^2}{BD^2}\) => đpcm
???