Cho hàm số y=\(\sqrt{2x-x^2}\) , tính giá trị biểu thức A=y3.yn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 10 2023
a) \(A=x^3+y^3+3xy\)
\(=x^3+y^3+3xy\left(x+y\right)\) (do \(x+y=1\))
\(=x^3+3x^2y+3xy^2+y^3\)
\(=\left(x+y\right)^3\) \(=1\)
b) \(B=x^3-y^3-3xy\)
\(=x^3-y^3-3xy\left(x-y\right)\) (do \(x-y=1\))
\(=x^3-3x^2y+3xy^2-y^3\)
\(=\left(x-y\right)^3\) \(=1\)
T
15 tháng 10 2023
\(a,A=x^2+y^2\\=x^2-2xy+y^2+2xy\\=(x-y)^2+2xy\\=2^2+2\cdot1\\=4+2\\=6\)
\(b,x+y=1\\\Leftrightarrow (x+y)^3=1^3\\\Leftrightarrow x^3+3x^2y+3xy^2+y^3=1\\\Leftrightarrow x^3+3xy(x+y)+y^3=1\\\Leftrightarrow x^3+3xy\cdot1+y^3=1\\\Rightarrow A=1\)
P
Phong
CTVHS
15 tháng 10 2023
a) Ta có:
\(x-y=2\)
\(\Rightarrow\left(x-y\right)^2=2^2\)
\(\Rightarrow x^2-2xy+y^2=4\)
Mà: \(xy=1\)
\(\Rightarrow\left(x^2+y^2\right)-2\cdot1=4\)
\(\Rightarrow x^2+y^2=4+2\)
\(\Rightarrow x^2+y^2=6\)
b) Ta có:
\(x+y=1\)
\(\Rightarrow\left(x+y\right)^3=1^3\)
\(\Rightarrow x^3+3x^2y+3xy+y^3=1\)
\(\Rightarrow x^3+3xy\left(x+y\right)+y^3=1\)
Mà: x + y = 1
\(\Rightarrow x^3+3xy\cdot1+y^3=1\)
\(\Rightarrow x^3+3xy+y^3=1\)
15 tháng 9
Câu 15:
1: Sửa đề: Chứng minh AH⊥BC
Xét (O) có
ΔBMC nội tiếp
BC là đường kính
Do đó: ΔBMC vuông tại M
=>CM⊥AB tại M
Xét (O) có
ΔBNC nội tiếp
BC là đường kính
Do đó: ΔBNC vuông tại N
=>BN⊥AC tại N
Gọi K là giao điểm của AH và BC
Xét ΔABC có
BN,CM là các đường cao
BN cắt CM tại H
Do đó: H là trực tâm của ΔABC
=>AH⊥BC tại K
2: ΔAMH vuông tại M
mà ME là đường trung tuyến
nên ME=EH=EA
ME=EH
=>ΔEMH cân tại E
=>\(\hat{EMH}=\hat{EHM}\)
mà \(\hat{EHM}=\hat{KHC}\) (hai góc đối đỉnh)
nên \(\hat{EMH}=\hat{KHC}\)
ΔOMC cân tại O
=>\(\hat{OMC}=\hat{OCM}\)
\(\hat{OME}=\hat{OMC}+\hat{EMC}\)
\(=\hat{OCM}+\hat{KHC}=90^0\)
=>ME⊥MO tại M
=>ME là tiếp tuyến của (O) tại M
3: ΔANH vuông tại N
mà NE là đường trung tuyến
nên NE=EH=EM
EM=EN nên E nằm trên đường trung trực của MN(1)
OM=ON
nên O nằm trên đường trung trực của MN(2)
Từ (1),(2) suy ra EO là đường trung trực của MN
=>EO⊥MN tại I và I là trung điểm của MN
Xét ΔEMO vuông tại M có MI là đường cao
nên \(MI\cdot EO=ME\cdot MO\)
=>\(2\cdot ME\cdot MO=2\cdot MI\cdot EO=EO\cdot MN\)
Câu 14:
a: Sửa đề: Cho hàm số y=2x-4
Vẽ đồ thị:
b: Thay x=0 vào y=x-3, ta được:
y=0-3=-3
=>A(0;-3)
Thay y=0 vào y=2x+1, ta được:
2x+1=0
=>2x=-1
=>\(x=-\frac12\)
=>B(-1/2;0)
Thay x=0 và y=-3 vào y=ax+b, ta được:
\(a\cdot0+b=-3\)
=>b=-3
=>y=ax-3
Thay x=-1/2 và y=0 vào y=ax-3, ta được:
\(a\cdot\frac{-1}{2}-3=0\)
=>\(-\frac12a=3\)
=>a=-6
HB
1
HB
3
18 tháng 7 2023
A=2(x3-y3)-3(x+y)2
A=2(x-y)(x2+xy+y2)-3(x2+2xy+y2)
A=2.2(x2+xy+y2)-3(x2+2xy+y2)
A=4(x2+xy+y2)-3x2+6xy+3y2
A=4x2+4xy+y2-3x2-6xy+3y2
A=x2-2xy+y2
A=(x-y)2
A= 22
A=4
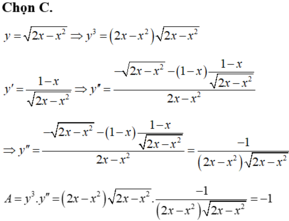
\(y^3y^n\) là gì hả bạn?