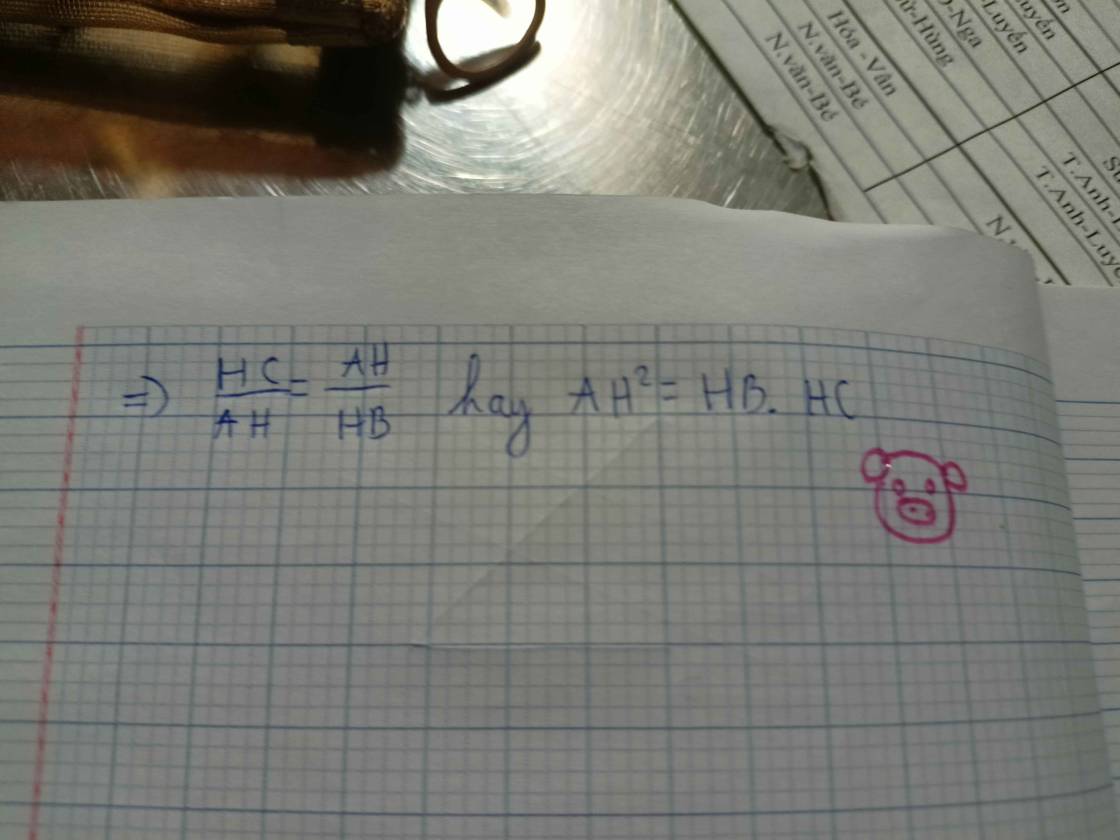Cho \(\Delta\)A'B'C', \(\Delta\)ABC có A'M', AM là trung tuyến. Cho biết \(\dfrac{A'B'}{AB}\)=\(\dfrac{A'M'}{AM}\)=\(\dfrac{A'C'}{AC}\). Chứng minh: \(\Delta\)A'B'C' đồng dạng với \(\Delta\)ABC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 3 2023
a)xét ΔABC và ΔHBA ta có
\(\widehat{BAH}=\widehat{BHA}=90^o\)
\(\widehat{B}chung\)
=>ΔABC ∼ ΔHBA(g.g)(1)
b)xét ΔABC và ΔAHC ta có
\(\widehat{BAC}=\widehat{AHC}=90^o\)
\(\widehat{B}chung\)
->ΔABC ∼ ΔAHC(g.g)(2)
từ (1) và (2)=>ΔHBA và ΔAHC
->\(\dfrac{AH}{BH}=\dfrac{HC}{AH}\)
=>\(AH^2=BH.HC\)
17 tháng 12 2021
a) Nối A và D lại, ta đc: ΔABD & ΔADC
Ta có: D là trung điểm BC => BD=DC
Xét ΔABD & ΔADC có:
AB=AC(gt) ; BD=DC ; AD=AD
=> ΔADB = ΔADC
TM
17 tháng 12 2021
1a. Xét △ABD và △ACD có:
\(AB=BC\left(gt\right)\)
\(\hat{BAD}=\hat{CAD}\left(gt\right)\)
\(AD\) chung
\(\Rightarrow\Delta ABD=\Delta ACD\left(c.g.c\right)\)
b/ Từ a suy ra \(BD=CD\) (hai cạnh tương ứng).
2a. Xét △ABD và △EBD có:
\(AB=BE\left(gt\right)\)
\(\hat{ABD}=\hat{EBD}\left(gt\right)\)
\(BD\) chung
\(\Rightarrow\Delta ABD=\Delta EBD\left(c.g.c\right)\)
b/ Từ a suy ra \(\hat{DEB}=90^o\) (góc tương ứng với góc A).
c/ Xét △ABI và △EBI có:
\(AB=BE\left(gt\right)\)
\(\hat{ABI}=\hat{EBI}\left(do\text{ }\hat{ABD}=\hat{EBD}\right)\)
\(BI\) chung
\(\Rightarrow\Delta ABI=\Delta EBI\left(c.g.c\right)\)
\(\Rightarrow\hat{AIB}=\hat{EIB}=\dfrac{180^o}{2}=90^o\)
Vậy: \(BD\perp AE\)
26 tháng 4 2020
a) Xét ΔABD vuông tại A và ΔFBD vuông tại F có
BD là cạnh chung
BA=BF(gt)
Do đó: ΔABD=ΔFBD(cạnh huyền-cạnh góc vuông)
b) Xét ΔAED vuông tại A và ΔFCD vuông tại F có
DA=DF(ΔABD=ΔFBD)
\(\widehat{ADE}=\widehat{FDC}\)(hai góc đối đỉnh)
Do đó: ΔAED=ΔFCD(cạnh góc vuông-góc nhọn kề)
⇒AE=FC(hai cạnh tương ứng)
Ta có: AE+AB=EB(A nằm giữa E và B)
FC+FB=BC(F nằm giữa B và C)
mà AE=FC(cmt)
và AB=FB(gt)
nên EB=BC
Xét ΔABC vuông tại A và ΔFEB vuông tại F có
BC=EB(cmt)
BA=BF(gt)
Do đó: ΔABC=ΔFEB(cạnh huyền-cạnh góc vuông)
27 tháng 12 2017
A B C D M
a) Xét tam giác ABC và tam giác ABD cùng vuông tại A, ta có :
BA là cạnh chung
DA=AC ( Giả thiết )
=> Tam giác ABC = Tam giác ABD ( Cạnh vuông-cạnh vuông )
b) Xem lại đề.
14 tháng 6 2022
a: Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
góc BAH chung
Do đó ΔABH=ΔACK
b: Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\)
nên ΔOBC cân tại O
c: Xét ΔOBK vuông tại K và ΔOCH vuông tại H có
OB=OC
KB=HC
Do đó:ΔOBK=ΔOCH
HQ
Hà Quang Minh
Giáo viên
10 tháng 9 2023
Khẳng định d) là khẳng định không đúng
=> ΔACB \(\backsim\) ΔMPN