Bài 1: Cho tam giác ABC; M là trung điểm AB; N thuộc AC sao cho NC = 2NA. Xác định K, D sao cho:
a. 3\(\overrightarrow{AB}\) + 2\(\overrightarrow{AC}\) - 12 \(\overrightarrow{AK}\) = \(\overrightarrow{0}\)
b. \(3\)\(\overrightarrow{AB}+4\overrightarrow{AC}-12\overrightarrow{KD}=\overrightarrow{0}\)
Bài 2: Cho tứ giác ABCD. Xác định G sao cho: \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GD}=\overrightarrow{0}\)
Chứng minh G là duy nhất
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan

12 tháng 5 2022
a: Input: a,b,c
Output: a+b+c
b: Bước 1: Nhập a,b,c
Bước 2: Xuất a+b+c
Bước 3: kết thúc
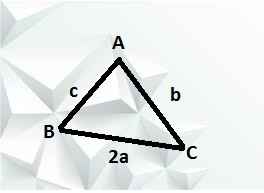 cho hình tam giác ABC và độ dài ba cạnh của tam giác như hình vẽ . tính chu vi của tam giác ABC
cho hình tam giác ABC và độ dài ba cạnh của tam giác như hình vẽ . tính chu vi của tam giác ABC
Bài 2:
Gọi M là trung điểm của AB,N là trung điểm của CD
vecto GA+vecto GB+vecto GC+vecto GD=vecto 0
=>2 vetco GM+2 vecto GN=vecto 0
=>vecto GM+vecto GN=vecto 0
=>G là trung điểm của MN