gtnn biểu thức x4+3x2-4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
0
CM
30 tháng 7 2019
Ta có
( x 2 + 3 ) ( x 4 – 3 x 2 + 9 ) = ( x 2 + 3 ) x 2 2 - 3 x 2 + 3 2 = x 2 3 + 3 3
Đáp án cần chọn là: A
VM
20 tháng 3 2022
a, Có \(\left(x^2-9\right)^2\)≥0 ∀ x ∈ Z
|y-2| ≥0 ∀ y ∈ Z
⇒ Gía trị nhỏ nhất A=-1. Dấu ''='' xảy ra khi:\(\left(x^2-9\right)^2\)+|y-2|=0
⇒ \(x=3\) ; \(y=2\)
Vậy.....
b, Có \(x^4\) ≥ 0 ∀ x ∈ Z
3\(x^2\) ≥ 0 ∀ x ∈ Z
⇒ Giá trị nhỏ nhất của B=2. Dấu ''='' xảy ra khi: \(x^4\)+3\(x^2\)=0
⇒ \(x^2\left(x^2+3\right)\)=0
⇒ \(x^2\) =0
⇒ \(x=0\)
Vậy...
TH
1
MH
17 tháng 10 2023
Sửa đề:
\(E=x^4-2x^3+3x^2-4x+2022\)
\(=\left(x^4-2x^3+x^2\right)+\left(2x^2-4x+2\right)+2020\)
\(=\left(x^2-x\right)^2+2\left(x-1\right)^2+2020\)
Vì \(\left(x^2-x\right)^2+2\left(x-1\right)^2\ge0\forall x\)
\(\Rightarrow E\ge2020\)
\(MinE=2020\Leftrightarrow\left\{{}\begin{matrix}x^2-x=0\\x-1=0\end{matrix}\right.\)\(\Leftrightarrow x=1\)
CM
31 tháng 10 2019
Thu gọn Q(x) = x4 + 7x2 + 1
Khi đó R(x) = Q(x) - P(x) = 4x2 + 3x + 2. Chọn A
22 tháng 8 2023
a) \(...=P\left(x\right)=2x^4-x^4+3x^3+4x^2-3x^2+3x-x+3\)
\(P\left(x\right)=x^4+3x^3+x^2+2x+3\)
\(...=Q\left(x\right)=x^4+x^3+3x^2-x^2+4x+4-2\)
\(Q\left(x\right)=x^4+x^3+2x^2+4x+2\)
b) \(P\left(x\right)+Q\left(x\right)=\left(x^4+3x^3+x^2+2x+3\right)+\left(x^4+x^3+2x^2+4x+2\right)\)
\(\Rightarrow P\left(x\right)+Q\left(x\right)=2x^4+4x^3+3x^2+6x+5\)
\(P\left(x\right)-Q\left(x\right)=\left(x^4+3x^3+x^2+2x+3\right)-\left(x^4+x^3+2x^2+4x+2\right)\)
\(\)\(\Rightarrow P\left(x\right)-Q\left(x\right)=x^4+3x^3+x^2+2x+3-x^4-x^3-2x^2-4x-2\)
\(\Rightarrow P\left(x\right)-Q\left(x\right)=2x^3-x^2-2x+1\)
29 tháng 5 2022
3: \(x^4-13x^2+36\)
\(=x^4-9x^2-4x^2+36\)
\(=\left(x^2-9\right)\left(x^2-4\right)\)
\(=\left(x-3\right)\left(x+3\right)\left(x-2\right)\left(x+2\right)\)
4: \(x^4+3x^2-2x+3\)
\(=x^4+x^3+3x^2-x^3-x^2-3x+x^2+x+3\)
\(=\left(x^2+x+3\right)\left(x^2-x+1\right)\)
5: \(x^4+2x^3+3x^2+2x+1\)
\(=x^4+x^3+x^2+x^3+x^2+x+x^2+x+1\)
\(=\left(x^2+x+1\right)^2\)
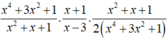
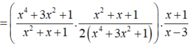
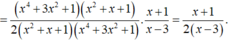
\(x^4\ge0;3x^2\ge0;=>x^4+3x^2\ge0=>x^4+3x^2-4\ge0-4=-4\)
vậy GTNN là -4