giúp mình với 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

15 tháng 12 2021
a. Chu vi là \(\left(12+5\right).2=34\left(m\right)\)
Diện tích là \(12.5=60\left(m^2\right)=600000\left(cm^2\right)\)
b. Cần lát \(600000:\left(40.40\right)=375\) viên gạch

17 tháng 3 2022
TL:
Sai nhé bạn
Bạn k cho mik cái đi nhé
@@@@@@@@@@@@@@@@@
HT

IO
13 tháng 12 2021
3x . 2 + 15 = 33
3x . 2 = 33 - 15 = 18
3x = 18 : 2 = 9 = 32
=> x = 2
NT
0




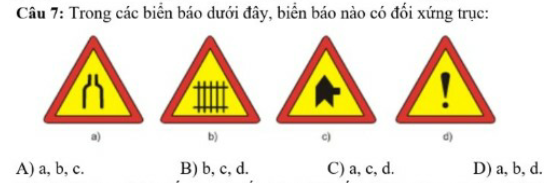
 Ai giúp mình với ạ
Ai giúp mình với ạ
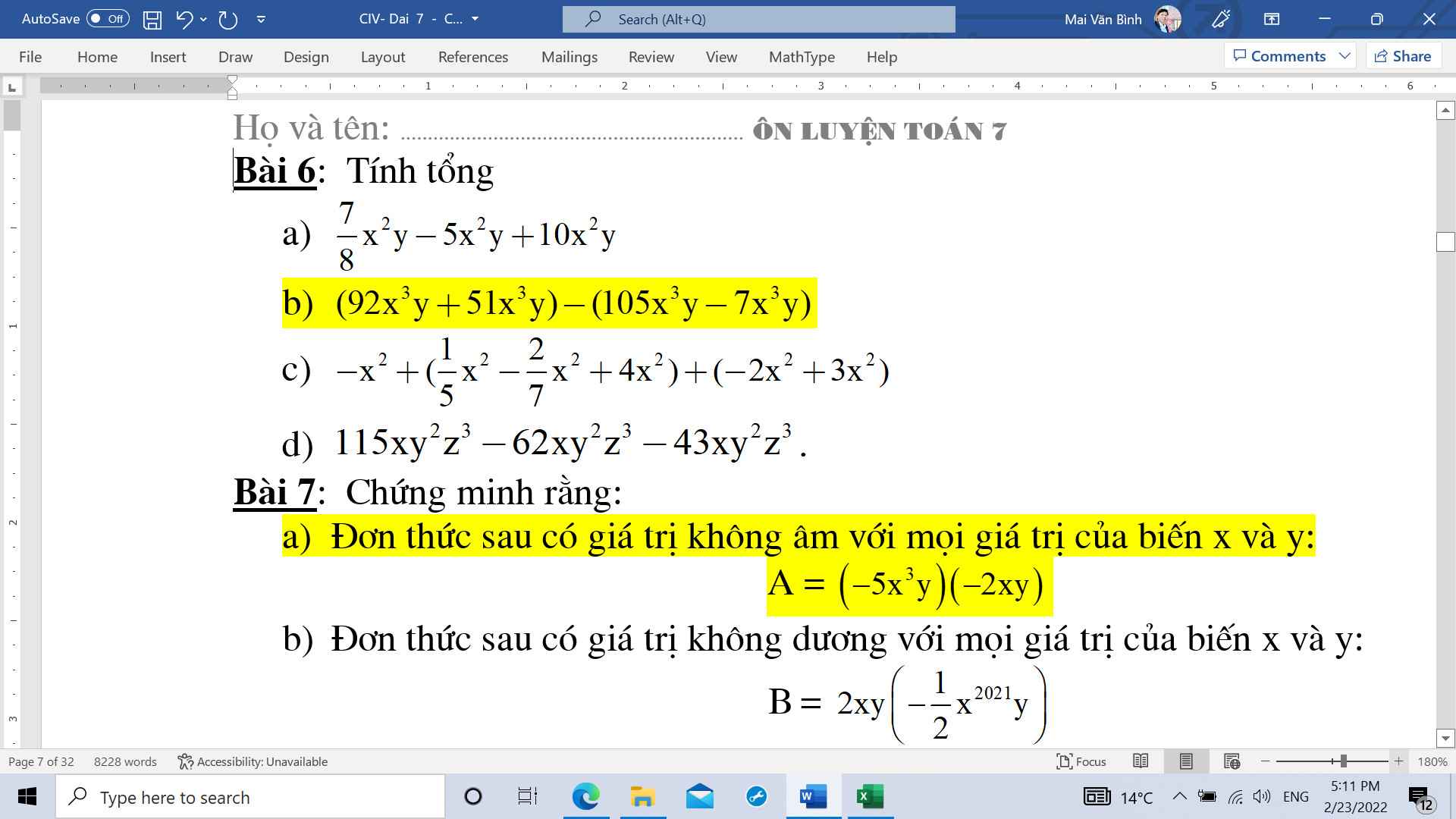
Ta có : \(\sqrt{x}+\sqrt{y-1}+\sqrt{z-2}=\frac{x+y+z}{2}\)(ĐKXĐ : \(x\ge0;y\ge1;z\ge2\))
\(\Leftrightarrow2\sqrt{x}+2\sqrt{y-1}+2\sqrt{z-2}=x+y+z\)
\(\Leftrightarrow\left(x-2\sqrt{x}+1\right)+\left(y-1-2\sqrt{y-1}+1\right)+\left(z-2-2\sqrt{z-2}+1\right)=0\)\(\Leftrightarrow\left(\sqrt{x}-1\right)^2+\left(\sqrt{y-1}-1\right)^2+\left(\sqrt{z-2}-1\right)^2=0\) (1)
Mà \(\left(\sqrt{x}-1\right)^2\ge0\); \(\left(\sqrt{y-1}-1\right)^2\ge0\) ; \(\left(\sqrt{z-2}-1\right)^2\ge0\)
Suy ra : (1) \(\Leftrightarrow\begin{cases}\left(\sqrt{x}-1\right)^2=0\\\left(\sqrt{y-1}-1\right)^2=0\\\left(\sqrt{z-2}-1\right)^2=0\end{cases}\) \(\Leftrightarrow\begin{cases}x=1\\y=2\\z=3\end{cases}\) (TMĐK)
Vậy \(\left(x_0;y_0;z_0\right)=\left(1;2;3\right)\)
\(S=x_0^2+y_0^2+z_0^2=1^2+2^2+3^2=14\)