bài 2:giải các phương trình sau
a,x^3+x^2+x=-1/3
b,x^3+x^2-x+2=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NT
1
Những câu hỏi liên quan
NT
2
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 7 2021
a.
\(\Leftrightarrow3x^3+3x^2+3x=-1\)
\(\Leftrightarrow x^3+3x^2+3x+1=-2x^3\)
\(\Leftrightarrow\left(x+1\right)^3=\left(-\sqrt[3]{2}x\right)^3\)
\(\Leftrightarrow x+1=-\sqrt[3]{2}x\)
\(\Leftrightarrow\left(1+\sqrt[3]{2}\right)x=-1\)
\(\Leftrightarrow x=-\dfrac{1}{1+\sqrt[3]{2}}\)
b.
\(\Leftrightarrow x^3-x^2+x+2x^2-2x+2=0\)
\(\Leftrightarrow x\left(x^2-x+1\right)+2\left(x^2-x+1\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(x^2-x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+2=0\Rightarrow x=-2\\x^2-x+1=0\left(vn\right)\end{matrix}\right.\)
25 tháng 7 2021
b) Ta có: \(x^3+x^2-x+2=0\)
\(\Leftrightarrow x^3+2x^2-x^2-2x+x+2=0\)
\(\Leftrightarrow x^2\left(x+2\right)-x\left(x+2\right)+\left(x+2\right)=0\)
\(\Leftrightarrow x+2=0\)
hay x=-1
DT
23 tháng 2 2022
a/
\(\left(x-1\right)^2-\left(x+1\right)^2=2x-6\\ x^2-2x+1-\left(x^2+2x+1\right)=2x-6\\ \)
\(\Leftrightarrow x^2-2x+1-x^2-2x-1-2x+6=0\)
\(\Leftrightarrow6-6x=0\)
=> x=1
MB
Giải các phương trình sau
a)\(x^2-2-x+\sqrt{2}=0\)
b) \((1-\sqrt{2})x^2-2(1+\sqrt{2})x+1+3\sqrt{2}=0\)
1
2 tháng 1 2024
a: \(x^2-2-x+\sqrt{2}=0\)
=>\(\left(x-\sqrt{2}\right)\left(x+\sqrt{2}\right)-\left(x-\sqrt{2}\right)=0\)
=>\(\left(x-\sqrt{2}\right)\left(x+\sqrt{2}-1\right)=0\)
=>\(\left[{}\begin{matrix}x=\sqrt{2}\\x=-\sqrt{2}+1\end{matrix}\right.\)
b: \(\left(1-\sqrt{2}\right)x^2-2\left(1+\sqrt{2}\right)x+1+3\sqrt{2}=0\)
\(\Delta=\left(-2-2\sqrt{2}\right)^2-4\left(1-\sqrt{2}\right)\left(1+3\sqrt{2}\right)\)
\(=12+8\sqrt{2}+4\left(\sqrt{2}-1\right)\left(3\sqrt{2}+1\right)\)
\(=12+8\sqrt{2}+4\left(6+\sqrt{2}-3\sqrt{2}-1\right)\)
\(=12+8\sqrt{2}+24-8\sqrt{2}-4=32>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{2\left(1+\sqrt{2}\right)-4\sqrt{2}}{2\left(1-\sqrt{2}\right)}=1\\x_2=\dfrac{2\left(1+\sqrt{2}\right)+4\sqrt{2}}{2\left(1-\sqrt{2}\right)}=-7-4\sqrt{2}\end{matrix}\right.\)
AT
6 tháng 6 2021
a) ĐKXĐ: \(x^2-1\ge0\)
Đặt \(\sqrt{x^2-1}=t\left(t\ge0\right)\)
\(\Rightarrow t=t^2\Rightarrow t\left(t-1\right)=0\Rightarrow\left[{}\begin{matrix}t=0\\t=1\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}\sqrt{x^2-1}=0\\\sqrt{x^2-1}=1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\pm1\\x=\pm\sqrt{2}\end{matrix}\right.\)
b) ĐKXĐ: \(x\ge2\)
Ta có: \(\sqrt{x-2}+\sqrt{x-3}\ge0\) mà \(\sqrt{x-2}+\sqrt{x-3}=-5< 0\Rightarrow\) không có x thỏa
c) \(\sqrt{x^2+4x+4}+\left|x-4\right|=0\)
\(\Rightarrow\left|x+2\right|+\left|x-4\right|=0\) mà \(\left|x+2\right|+\left|x-4\right|\ge0\Rightarrow\left\{{}\begin{matrix}x+2=0\\x-4=0\end{matrix}\right.\)
\(\Rightarrow\) không có x thỏa
17 tháng 9
a: \(\left(9x^2-4\right)\left(x+1\right)=\left(3x+2\right)\left(x^2-1\right)\)
=>\(\left(3x-2\right)\left(3x+2\right)\left(x+1\right)-\left(3x+2\right)\left(x-1\right)\left(x+1\right)=0\)
=>(3x+2)(x+1)(3x-2-x+1)=0
=>(3x+2)(x+1)(2x-1)=0
=>\(\left[\begin{array}{l}3x+2=0\\ x+1=0\\ 2x-1=0\end{array}\right.\Rightarrow\left[\begin{array}{l}x=-\frac23\\ x=-1\\ x=\frac12\end{array}\right.\)
c: \(\left(x-1\right)^2-1+x^2=\left(1-x\right)\left(x+3\right)\)
=>\(x^2-2x+1-1+x^2=-\left(x-1\right)\left(x+3\right)\)
=>\(2x^2-2x+\left(x-1\right)\left(x+3\right)=0\)
=>2x(x-1)+(x-1)(x+3)=0
=>(x-1)(3x+3)=0
=>3(x-1)(x+1)=0
=>(x-1)(x+1)=0
=>\(\left[\begin{array}{l}x-1=0\\ x+1=0\end{array}\right.\Rightarrow\left[\begin{array}{l}x=1\\ x=-1\end{array}\right.\)
e: \(x^3-7x+6=0\)
=>\(x^3-x-6x+6=0\)
=>\(x\left(x^2-1\right)-6\left(x-1\right)=0\)
=>x(x-1)(x+1)-6(x-1)=0
=>\(\left(x-1\right)\left(x^2+x-6\right)=0\)
=>(x-1)(x+3)(x-2)=0
=>\(\left[\begin{array}{l}x-1=0\\ x+3=0\\ x-2=0\end{array}\right.\Rightarrow\left[\begin{array}{l}x=1\\ x=-3\\ x=2\end{array}\right.\)
g: \(x^5-5x^3+4x=0\)
=>\(x\left(x^4-5x^2+4\right)=0\)
=>\(x\left(x^2-1\right)\left(x^2-4\right)=0\)
=>\(\left[\begin{array}{l}x=0\\ x^2-1=0\\ x^2-4=0\end{array}\right.\Rightarrow\left[\begin{array}{l}x=0\\ x^2=1\\ x^2=4\end{array}\right.\Rightarrow\left[\begin{array}{l}x=0\\ x=1\\ x=-1\\ \left[\begin{array}{l}x=2\\ x=-2\end{array}\right.\end{array}\right.\)
HH
1
NA
Ngoc Anh Thai
Giáo viên
15 tháng 5 2021
a)
\(2x-1+5\left(3-x\right)>0\\ 2x-2+15-5x>0\\ -3x+13>0\\ x< \dfrac{13}{3}.\)
B
Bài 1: Giải các bất phương trình sau
a) x+1/x+3 > 1
b) 2x-1/x-3 ≤ 2
c) x2+2x+2/x2+3 ≥ 1
d) 2x+1/x2+2 ≥ 1
2
13 tháng 4 2021
a, \(\dfrac{x+1}{x+3}>1\Leftrightarrow\dfrac{x+1}{x+3}-1>0\Leftrightarrow\dfrac{x+1-x-3}{x+3}>0\)
\(\Rightarrow x+3< 0\)do -2 < 0
\(\Rightarrow x< -3\)Vậy tập nghiệm BFT là S = { x | x < -3 }
b, \(\dfrac{2x-1}{x-3}\le2\Leftrightarrow\dfrac{2x-1}{x-3}-2\le0\Leftrightarrow\dfrac{2x-1-2x+6}{x-3}\le0\)
\(\Rightarrow x-3\le0\)do 5 > 0
\(\Rightarrow x\le3\)Vậy tập nghiệm BFT là S = { x | x \(\le\)3 }
c, \(\dfrac{x^2+2x+2}{x^2+3}\ge1\Leftrightarrow\dfrac{x^2+2x+2}{x^2+3}-1\ge0\)
\(\Leftrightarrow\dfrac{x^2+2x+2-x^2-3}{x^2+3}\ge0\Rightarrow2x-1\ge0\)do x^2 + 3 > 0
\(\Rightarrow x\ge\dfrac{1}{2}\)Vậy tập nghiệm BFT là S = { x | x \(\ge\)1/2 }
13 tháng 4 2021
mình ko chắc nên mình đăng sau :>
d, \(\dfrac{2x+1}{x^2+2}\ge1\Leftrightarrow\dfrac{2x+1}{x^2+2}-1\ge0\Leftrightarrow\dfrac{2x+1-x^2-2}{x^2+2}\ge0\)
\(\Rightarrow-x^2+2x-1\ge0\Rightarrow-\left(x-1\right)^2\ge0\)vô lí
NA
13 tháng 5 2022
\(a)2x-3=4x+6\\ \Rightarrow2x=-9\\ \Rightarrow x=-\dfrac{9}{2}\\ c)x\left(x-1\right)+x\left(x+3\right)=0\\ \Rightarrow x^2-x+x^2+3x=0\\ \Rightarrow2x^2+2x=0\\ \Rightarrow2x\left(x+1\right)=0\\ \Rightarrow\left[{}\begin{matrix}2x=0\\x+1=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=0\\x=-1\end{matrix}\right.\)
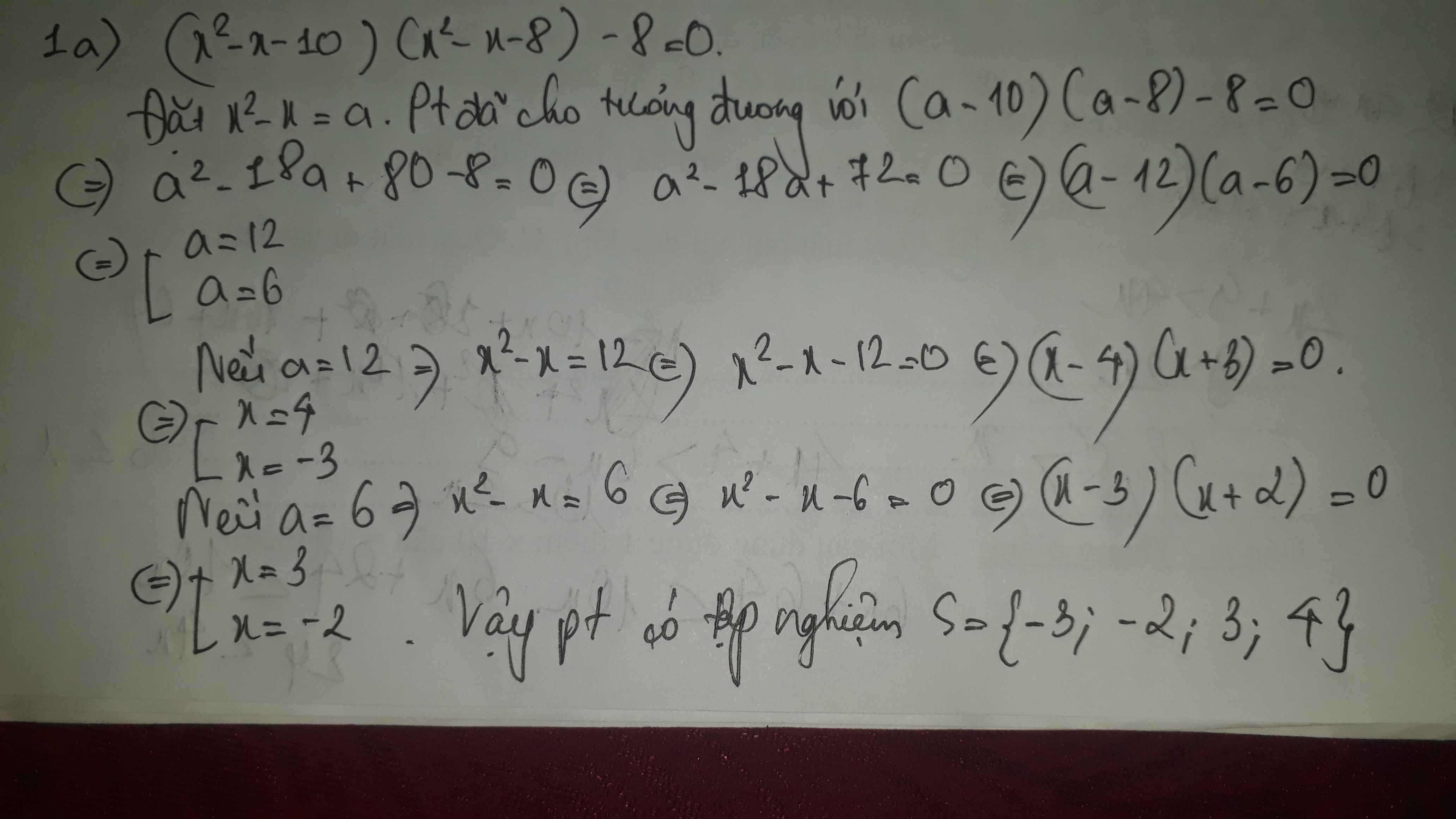
b) Ta có: \(x^3+x^2-x+2=0\)
\(\Leftrightarrow x^3+2x^2-x^2-2x+x+2=0\)
\(\Leftrightarrow x^2\left(x+2\right)-x\left(x+2\right)+\left(x+2\right)=0\)
\(\Leftrightarrow x+2=0\)
hay x=-2