Cho hàm số y = f(x) liên tục trên đoạn [a;b]. Diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số y = f(x), trục hoành và hai đường thẳng x = a, x = b (a<b) được tính theo công thức:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương pháp: Sử dụng phương pháp đổi biến, đặt t = u(x)
Cách giải:
Đặt
![]()
Đổi cận 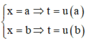
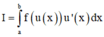


Ta có
![]()
![]()
![]()
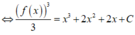
![]()
Ta có: f ( 0 ) = 1 ⇒ 1 = 3 C
![]()
![]()
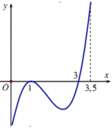
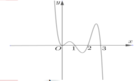
Xét hàm ![]() trên [-2;1]
trên [-2;1]
Ta có
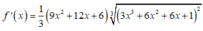
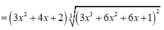
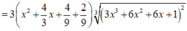
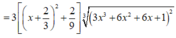
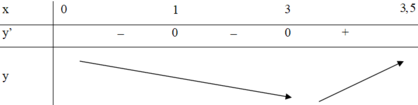
Nhận thấy f ' ( x ) > 0 ∀ x ∈ ℝ ⇒ Hàm số đồng biến trên (-2;1)
Suy ra m a x - 2 ; 1 f ( x ) = f ( 1 ) = 16 3
Chọn đáp án C.

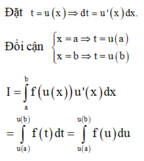
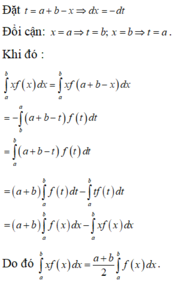
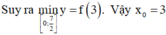
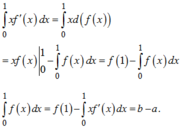

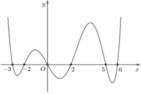

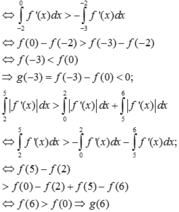
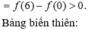
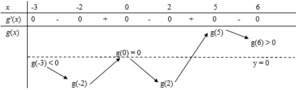

Đáp án A
Phương pháp:
Diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số y = f(x), trục hoành và hai đường thẳng x = a, x= b (a<b) được tính theo công thức S = ∫ a b f ( x ) d x
Cách giải:
Diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số y = f(x), trục hoành và hai đường thẳng x = a, x= b (a<b) được tính theo công thức S = ∫ a b f ( x ) d x