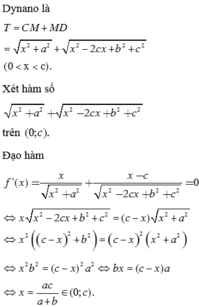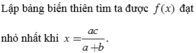Từ hai vị trí quan sát A và B của một tòa nhà

TN

Trọng Nghĩa Nguyễn

15 tháng 12 2022

Từ hai vị trí quan sát A và B của một tòa nhà; người ta quan sát đỉnh C của ngọn núi. Biết rằng độ cao AB = 70m, phương nhìn AC tạo với phương nằm ngang một góc 30°, phương nhìn BC tạo với phương nằm ngang một góc 15°30' . Tính chiều cao của ngọn...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 10

0

AD

Anh Dao

14 tháng 10 2021

Một người quan sát đỉnh một tòa nhà tại hai vị trí cách nhau 12m với các góc nâng là 0 20 và 0 35 (xem hình). Hỏi chiều cao của tòa nhà là bao nhiêu? (làm tròn đến chữ số thập phân thứ hai)

#Hỏi cộng đồng OLM #Toán lớp 9

2

AD

Anh Dao

14 tháng 10 2021

e đang cần gấp mn ạ

Đúng(0)

NH

Nguyễn Hoàng Minh

14 tháng 10 2021

Hai vị trí cách nhau 12m tức là \(AB=12\left(m\right)\)

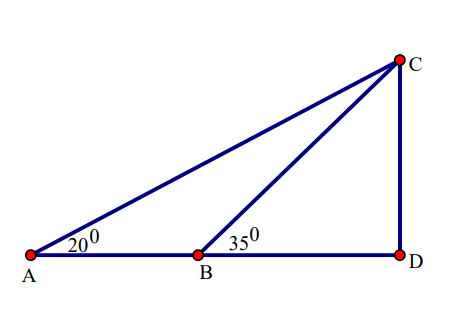
Ta có \(\tan\widehat{A}=\dfrac{CD}{AD}=\tan20^0\approx0,4\Leftrightarrow AD=\dfrac{CD}{0,4}\)

\(\tan\widehat{CBD}=\dfrac{CD}{BD}=\tan35^0\approx0,7\Leftrightarrow BD\approx\dfrac{CD}{0,7}\)

Ta có \(AD-BD=AB=12\)

\(\Leftrightarrow\dfrac{CD}{0,4}-\dfrac{CD}{0,7}=12\Leftrightarrow CD=\dfrac{56}{5}=11,2\left(m\right)\)

Vậy...

Đúng(1)

BT

Bình Trần Thị

6 tháng 12 2015

trên nóc 1 tòa nhà có một cột ăng - ten cao 5m . Từ vị trí quan sát A cao 7m so với mặt đất , có thể nhìn thấy đỉnh B và chân C của cột ăng - ten dưới góc 50⁰ và 40⁰ so với phương nằm ngang . Tính chiều cao của tòa nhà

#Hỏi cộng đồng OLM #Toán lớp 10

1

NT

Nguyễn Thắng Tùng

1 tháng 3 2016

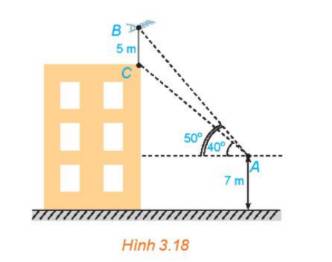
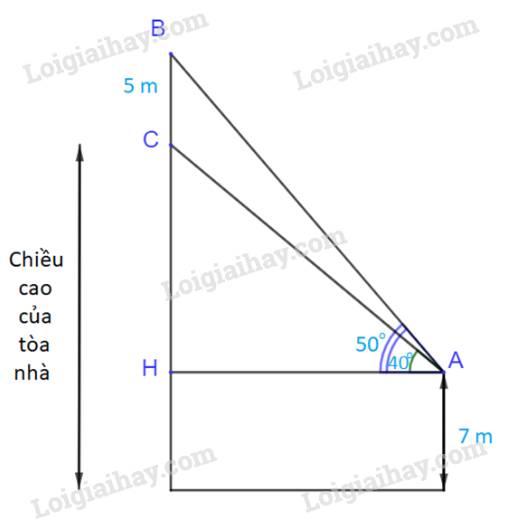
ve hinh thang vuong ABED co AD//BC ; va ED vuong goc voi BC keo dai ;
E thuoc BC keo dai(hinh chieu cua BC tren mat dat)
.D la diem duoi mat dat cua A AD=7m; BC=5m
Cac goc 40 ; 50 do la giua AC ; AB voi phuong nam ngang .
Ta tinh duoc DE theo BC : DE =BC/(tan50-tan40)
=> Bc da biet tan ta tra duoc .Con CE la chieu cao cua nha :
Vay : CE=AD+DE*tan40= 7+5*tan40/(tan50-tan40)

Đúng(0)

QT

Quoc Tran Anh Le

Giáo viên

24 tháng 9 2023

Một người đi dọc bờ biển từ vị trí A đến vị trí B và quan sát một ngọn hải đăng. Góc nghiêng của phương quan sát từ các vị trí A, B tới ngọn hải đăng với đường đi của người quan sát là \({45^o}\) và \({75^o}\). Biết khoảng cách giữa hai vị trí A, B là 30 m (Hình 32). Ngọn hải đăng cách bờ biển bao nhiêu mét (làm tròn kết quả đến hàng đơn...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 10

1

HQ

Hà Quang Minh

Giáo viên

24 tháng 9 2023

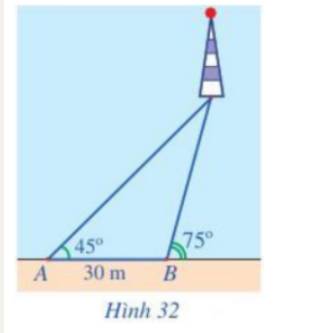
Gọi C là vị trí ngọn hải đăng và H là hình chiếu của C trên AB.

Khi đó CH là khoảng cách từ ngọn hải đăng tới bờ biển.

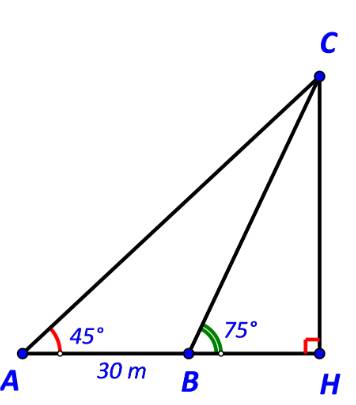
Ta có: \( \widehat {ACB} = \widehat {HBC} - \widehat {BAC} = {75^o} - {45^o} = {30^o}; \, \widehat {ABC} = {180^o} - {75^o} = {105^o}\)

Áp dụng định lí sin trong tam giác ABC ta có:

\(\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}}\)

\( \Rightarrow AC = \sin B.\frac{{AB}}{{\sin C}} = \sin {105^o}.\frac{{30}}{{\sin {{30}^o}}} \approx 58\)

Tam giác ACH vuông tại H nên ta có:

\(CH = \sin A.AC = \sin {45^o}.58 \approx 41\)

Vậy ngọn hải đăng cách bờ biển 41 m.

Đúng(0)

QT

Quoc Tran Anh Le

Giáo viên

24 tháng 9 2023

Trên nóc một tòa nhà có một cột ăng-ten cao 5m. Từ một vị trí quan sát A cao 7 m so với mặt đất có thể nhìn thấy đỉnh B và chân C của cột ăng-ten, với các góc tương ứng là \({50^o}\)và \({40^o}\) so với phương nằm ngang (H.3.18).a) Tính các góc của tam giác ABC.b) Tính chiều cao của tòa...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 10

1

KS

Kiều Sơn Tùng

24 tháng 9 2023

Tham khảo:

a)

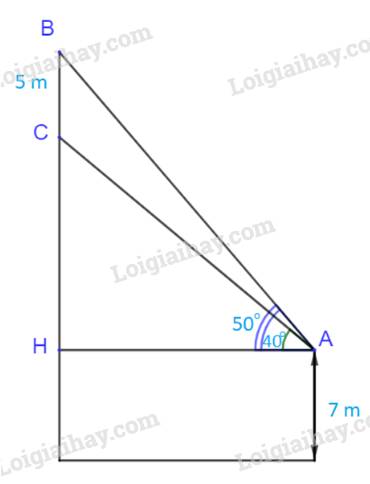
Gọi H là hình chiếu của A lên đường thẳng BC.

Ta có: \(\widehat {HAB} = {50^o}\); \(\widehat {HAC} = {40^o}\)

\( \Rightarrow \widehat {BAC} = {50^o} - {40^o} = {10^o}\) (1)

Xét tam giác ABH, vuông tại H ta có:

\(\widehat H = {90^o};\;\widehat {BAH} = {50^o}.\)

\( \Rightarrow \widehat {HBA} = {180^o} - {90^o} - {50^o} = {40^o}\) hay \(\widehat {CBA} = {40^o}\). (2)

Từ (1) và (2), suy ra: \(\widehat {BCA} = {180^o} - {40^o} - {10^o} = {130^o}.\)

Vậy ba góc của tam giác ABC lần lượt là: \(\widehat A = {10^o};\;\widehat B = {40^o};\;\widehat C = {130^o}\).

b)

Áp dụng định lý sin cho tam giác ABC, ta được:

\(\frac{{BC}}{{\sin A}} = \frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}}\) \( \Rightarrow AB = \frac{{BC.\sin C}}{{\sin A}}\)

Mà: \(BC = 5\;(m);\;\;\widehat C = {130^o};\;\widehat A = {10^o}\)

\( \Rightarrow AB = \frac{{5.\sin {{130}^o}}}{{\sin {{10}^o}}} \approx 22\;(m)\)

Xét tam giác ABH, vuông tại H ta có:

\(\sin \widehat {BAH} = \frac{{BH}}{{AB}}\)\( \Rightarrow BH = AB.\,\,\sin \widehat {BAH}\)

Mà: \(AB \approx 22\;(m);\;\;\widehat {BAH} = {50^o}\)

\( \Rightarrow BH \approx 22.\sin {50^o} \approx 16,85\;(m)\)

Vậy chiều cao của tòa nhà là: \(BH-{\rm{ }}BC + 7 = 16,85-5 + 7 = 18,85{\rm{ }}\left( m \right)\)

Đúng(0)

QT

Quoc Tran Anh Le

Giáo viên

24 tháng 9 2023

Từ trên nóc của một tòa nhà cao 18,5 m, bạn Nam quan sát một cái cây cách tòa nhà 30 m và dùng giác kế đo được góc lệch giữa phương quan sát gốc cây và phương nằm ngang là \({34^o}\), góc lệch giữa phương quan sát ngọn cây và phương nằm ngang là \({24^o}\). Biết chiều cao của chân giác kế là 1,5 m. Chiều cao của cái cây là bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?

#Hỏi cộng đồng OLM #Toán lớp 10

1

HQ

Hà Quang Minh

Giáo viên

24 tháng 9 2023

Gọi A là vị trí đứng của Nam, B là điểm cao nhất của cây, C là vị trí gốc cây.

Gọi H là hình chiếu của A trên BC. Ta có hình vẽ:

TH1: Cây cao hơn tòa nhà

Ta có: \(\tan {24^ \circ } = \frac{{BH}}{{AH}} \Rightarrow BH = 30.\tan {24^ \circ } \approx 13,357\)

\( \Rightarrow BC = BH + HC \approx 13,357 + 1,5 + 18,5 = 33,357(m)\)

TH2: Cây thấp hơn tòa nhà

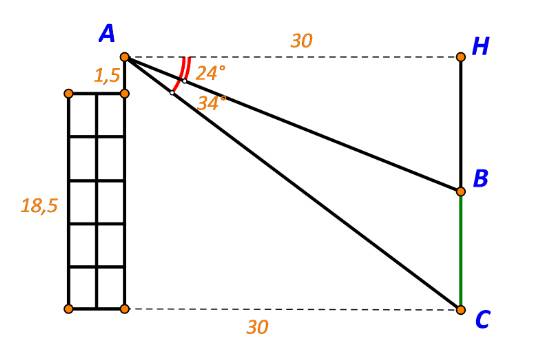
Ta có: \(\tan {24^ \circ } = \frac{{BH}}{{AH}} \Rightarrow BH = 30.\tan {24^ \circ } \approx 13,357\)

\( \Rightarrow BC = HC -HB \approx 1,5 + 18,5 - 13,357= 6,643(m)\)

Đúng(0)

PT

Pham Trong Bach

27 tháng 3 2017

Dynano là một nhà ảo thuật gia đại tài người Anh nhưng người ta thường nói Dynano làm ma thuật chứ không phải làm ảo thuật. Bất kì màn trình diễn nào của anh chàng trẻ tuổi tài cao này khiến người xem kinh ngạc vì nó vượt qua giới hạn khoa học. Một lần đến NewYork anh ngẫu hứng trình diễn khả năng bay lơ lửng trong không trung của mình bằng cách di chuyển từ tòa nhà này đến tòa nhà...

Đọc tiếp

#Hỏi cộng đồng OLM #Mẫu giáo

1

CM

Cao Minh Tâm

27 tháng 3 2017

Đáp án C.

Màn biểu diễn của Dynano được biểu diễn theo mô hình bên

Cách 1: Áp dụng kiến thức “Giá trị lớn nhất – Giá trị nhỏ nhất của hàm số”

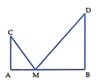
Ta có A B = c , A C = a , A D = b , A M = x . Khi đó C M = A C 2 + A M 2 = x 2 + a 2

Và

M D = B M 2 + B D 2 = ( c − x ) 2 + b 2 = x 2 − 2 c x + b 2 + c 2

Như vậy quãng đường di chuyển của Dynano là

T = C M + M D = x 2 + a 2 + x 2 − 2 c x + b 2 + c 2 ( 0 < x < c ) .

Xét hàm số x 2 + a 2 + x 2 − 2 c x + b 2 + c 2 trên ( 0 ; c ) .

Đạo hàm f ' ( x ) = x x 2 + a 2 + x − c x 2 − 2 c x + b 2 + c 2 = 0

⇔ x x 2 − 2 c x + b 2 + c 2 = ( c − x ) x 2 + a 2 ⇔ x 2 c − x 2 + b 2 = c − x 2 x 2 + a 2

⇔ x 2 b 2 = c - x 2 a 2 ⇔ b x = ( c − x ) a ⇔ x = a c a + b ∈ ( 0 ; c ) .

Lập bảng biến thiên tìm ta được f(x) đạt nhỏ nhất khi x = a c a + b .

Cách 2: Dùng kiến thức hình học

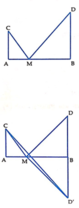
Gọi D' là điểm đối xứng với D qua AB. Khi đó M C + M D = M C + M D ' ≥ C D ' . Do vậy ( M C + M D ) min = C D ' . Dấu = xảy ra khi M ∈ C D ' hay M = C D ' ∩ A B .

Khi đó Δ A M C ∽ △ B M D '

⇒ A M B M = A C B D ' ⇔ x c − x = a b ⇔ x = a c a + b

Đúng(0)

PT

Pham Trong Bach

3 tháng 12 2017

Dynano là một nhà ảo thuật gia đại tài người Anh nhưng người ta thường nói Dynano làm ma thuật chứ không phải làm ảo thuật. Bất kì màn trình diễn nào của anh chàng trẻ tuổi tài cao này khiến người xem kinh ngạc vì nó vượt qua giới hạn khoa học. Một lần đến NewYork anh ngẫu hứng trình diễn khả năng bay lơ lửng trong không trung của mình bằng cách di chuyển từ tòa nhà này đến tòa nhà...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 12

1

CM

Cao Minh Tâm

3 tháng 12 2017

Đúng(0)

N

nini

23 tháng 12 2023

Câu 3. Hai người đứng ở vị trí A và B quan sát một máy bay trực thăng đang ở vị trí C với các góc lần lượt là 45° và 30° (như hình vẽ (bên dưới). Biết máy bay cách vị trí B là 260m. tính khoảng cách từ máy bay đến vị trị A 45 ° 30 ° C A B Câu 4. Cho đường tròn (O) đường kính AB = 2R. Trên đường tròn (O) lấy điểm C (C khác A, khác B) sao cho CA < CB. Tiếp tuyến tại A của...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

23 tháng 12 2023

Câu 3:

Xét ΔCAB có \(\dfrac{CB}{sinA}=\dfrac{CA}{sinB}\)

=>\(\dfrac{260}{sin45}=\dfrac{CA}{sin30}\)

=>\(CA\simeq183,85\left(m\right)\)

Câu 4:

a: Xét (O) có

ΔACB nội tiếp

AB là đường kính

Do đó: ΔCAB vuông tại C

=>AC\(\perp\)CB tại C

=>AC\(\perp\)EB tại C

Xét ΔABE vuông tại A có AC là đường cao

nên \(BC\cdot BE=BA^2=\left(2R\right)^2=4R^2\)

b: Ta có: ΔOAD cân tại O

mà OE là đường cao

nên OE là phân giác của góc AOD

Xét ΔOAE và ΔODE có

OA=OD

\(\widehat{AOE}=\widehat{DOE}\)

OE chung

Do đó: ΔOAE=ΔODE

=>\(\widehat{OAE}=\widehat{ODE}=90^0\)

Xét tứ giác EAOD có

\(\widehat{EAO}+\widehat{EDO}=90^0+90^0=180^0\)

=>EAOD là tứ giác nội tiếp

=>E,A,O,D cùng thuộc một đường tròn

c: Xét (O) có

OD là bán kính

ED\(\perp\)DO tại D

Do đó: ED là tiếp tuyến của (O)

Xét (O) có

\(\widehat{EDC}\) là góc tạo bởi tiếp tuyến DE và dây cung DC

\(\widehat{CBD}\) là góc nội tiếp chắn cung DC

Do đó: \(\widehat{EDC}=\widehat{CBD}\)

=>\(\widehat{EDC}=\widehat{EBD}\)

Xét ΔEDC và ΔEBD có

\(\widehat{EDC}=\widehat{EBD}\)

\(\widehat{DEC}\) chung

Do đó: ΔEDC đồng dạng với ΔEBD

=>\(\widehat{ECD}=\widehat{EDB}\)

Đúng(0)

PA

Phương Anh

20 tháng 1 2022

1. Công viên giҧi trí có một bộ sưu tập mô hình các toà nhà và những điểm tham quan khắp thành phố với tỉ lệ 1:20. Tòa nhà United States Capitol cao 289 feet. Hỏi chiều cao của mô hình tòa nhà này trong công viên theo đơn vị feet là bao nhiêu? Làm tròn tới số nguyên gần nhất.

#Hỏi cộng đồng OLM #Toán lớp 6

2

NK

Nguyễn Khánh Huyền

20 tháng 1 2022

mk nghĩ là 14.45 feet

Đúng(1)

PA

Phương Anh

20 tháng 1 2022

bạn ghi cách giải ra giúp mik với

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP