Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x (km) là độ dài quãng đường Ab, y (giờ) là thời gian dự định đi để đến B đúng lúc 12 giờ trưa. Điều kiện x > 0, y > 1 (do ôtô đến B sớm hơn 1 giờ).
Thời gian đi từ A đến B với vận tốc 35km là \(\frac{x}{35}\) = y + 2.
Thời gian đi từ A và B với vận tốc 50km là \(\frac{x}{50}\) = y - 1.
Ta có hệ phương trình: <=>\(\int^{\frac{x}{35}=y+2}_{\frac{x}{50}=y-1}\Leftrightarrow\int^{x=35\left(y+2\right)}_{y=50\left(y-1\right)}\)
Giải ra ta được: x = 350, y = 8.
Vậy quãng đường AB là 350km.
Thời điểm xuất phát của ô tô tại A là: 12 - 8 = 4 giờ.

Gọi x (km) là độ dài quãng đường Ab, y (giờ) là thời gian dự định đi để đến B đúng lúc 12 giờ trưa. Điều kiện x > 0, y > 1 (do ôtô đến B sớm hơn 1 giờ).
Thời gian đi từ A đến B với vận tốc 35km là \(\frac{x}{35}\) = y + 2.
Thời gian đi từ A và B với vận tốc 50km là \(\frac{x}{50}\) = y - 1.
Ta có hệ phương trình: <=>\(\int^{\frac{x}{35}=y+2}_{\frac{x}{50}=y-1}\Leftrightarrow\int^{x=35\left(y+2\right)}_{y=50\left(y-1\right)}\)
Giải ra ta được: x = 350, y = 8.
Vậy quãng đường AB là 350km.
Thời điểm xuất phát của ô tô tại A là: 12 - 8 = 4 giờ.

Gọi thời gian dự kiến mà xe ô tô sẽ đi từ A đến B là x(h)
(ĐIều kiện: x>0)
Độ dài quãng đường AB khi xe đi với vận tốc 35km/h là:
35(x+2)(km)
Độ dài quãng đường AB khi xe đi với vận tốc 50km/h là:
50(x-1)(km)
Do đó, ta có phương trình:
35(x+2)=50(x-1)
=>10(x-1)=7(x+2)
=>10x-10=7x+14
=>3x=24
=>x=8(nhận)
Thời điểm xuất phát của ô tô là:
12 giờ-8 giờ=4 giờ
Độ dài quãng đường AB là:
35(8+2)=35*10=350(km)

Gọi x ( km ) là độ dài quãng đường AB , y ( giờ ) là thời gian dự định đi từ A đến B đúng lúc 12h trưa .
Điều kiện : x > 0 ; y > 1 ( Vì do ô tô đến B sớm hơn 1h )
+) TH1 :
- Xe đi với vận tốc 35km/h
- Xe đến B chậm hơn 2h nên thời gian đi hết là : y + 2 ( giờ )
- Quãng đường đi được : 35 ( y + 2 ) km
- Vì quãng đường không thay đổi nên ta có phương trình : x = 35 ( y + 2 ) (1)
+) TH2
- Xe đi với vận tốc 50km/h
- Vì xe đến B sớm hơn 1h nên thời gian đi hết là : y - 1 ( giờ )
- Quãng đường đi được là : 50 . ( y - 1 ) ( km )
- Vì quãng đường không thay đổi nên ta có phương trình :
\(\hept{\begin{cases}x=35\left(y+2\right)\\x=50\left(y-1\right)\end{cases}\Leftrightarrow\hept{\begin{cases}x=35y+70\\x=50y-50\end{cases}}}\)
\(\Leftrightarrow\hept{\begin{cases}x-35y=70\left(3\right)\\x-50y=-50\left(4\right)\end{cases}}\)
- Lấy vế 1 trừ cho vế 2 , ta được :
\(\hept{\begin{cases}15y=120\\x-50y=-50\end{cases}\Leftrightarrow\hept{\begin{cases}y=8\\x=-50+50y\end{cases}}}\)
\(\Leftrightarrow\hept{\begin{cases}y=8\\x=-50+50.8\end{cases}\Leftrightarrow\hept{\begin{cases}y=8\\x=350\end{cases}\left(tmđk\right)}}\)
Vậy quãng đường AB là 350 km
Thời điểm xuất phát của ô tô tại A là :
12 − 8 = 4 giờ

Gọi x (km) là độ dài quãng đường AB,
y (giờ) là thời gian dự định đi đến B lúc đầu. (x>0,y>1)(Thời gian đi từ A đến B với vận tốc 35km là:
x35=y+2⇒x=35.(y+2)(1)Thời gian đi từ A và B với vận tốc 50km là: x50=y−1⇒x=50.(y−1)x50=y−1 (2)Từ (1) và (2) ta có:35.(y+2)=50.(y−1)⇒35y+70=50y−50⇒y=8⇒x=35.(y+2)=35.10=350 (km)
Vậy quãng đường AB là 350km và thời gian dự định đi lúc đầu là 8 giờ.

Gọi độ dài AB là x, thờigian dự định là y
Theo đề, ta có: x=35(y+2) và x=50(y-1)
=>x-35y=70 và x-50y=-50
=>x=350 và y=8

Đáp án D
Gọi vận tốc của ô tô là x (km/h)
Vận tốc của xe máy là y (km/h) ( Điều kiện: x > y > 0, x > 10)
Ta có vận tốc của ô tô lớn hơn vận tốc của xe máy 10 km/h nên : x – y = 10 (1)
Sau 2 giờ ô tô đi được quãng đường là 2x (km)
Sau 2 giờ xe máy đi được quãng đường là: 2y (km)
Sau 2 giờ thì chúng gặp nhau, ta có phương trình: 2x + 2y = 180 hay x + y = 90 (2)
Từ (1), (2) ta có hệ phương trình :
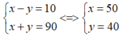
Thỏa mãn điều kiện,vậy vận tốc của ô tô là 50 km/h và vận tốc của xe máy là: 40 km/h

gọi s là quãng đường AB
nếu chạy với vận tốc 35km/h thì thời gian đi từ A đến B là s/35 và xe sẽ đến B lúc 14 giờ
nếu chạy với vận tốc 50km/h thì thời gian đi từ A đến B là s/50 và xe sẽ đến B lúc 11 giờ
=> s/35- s/50= 14 - 11 = 3 (giờ)
=> 10s/350 - 7s/350 = 3
=> s= 350 (km)
vậy quãng đường là 350 km
thời gian đi từ A đến B nếu xe đi với vận tốc 50km là 350/50= 7 giờ
vậy thời điểm xuất phát là 11-7=4 giờ
TL
Dưới đây là **lời giải chi tiết cho cả 4 câu toán**, bao gồm cách lập phương trình và kết quả.
---
## ✅ **Câu 1: Váy và quần**
**Đề bài:**
* Mua 10 váy + 25 quần hết **21.250.000 đồng**
* Biết **3 váy = 1 quần** (về giá tiền)
### 👣 **Bước 1: Đặt ẩn**
* Gọi giá **1 cái váy là x (đồng)**
→ Giá 1 quần = **3x** (vì 3 váy = 1 quần)
### 👣 **Bước 2: Lập phương trình**
$$
10x + 25 \cdot 3x = 21.250.000
\Rightarrow 10x + 75x = 21.250.000
\Rightarrow 85x = 21.250.000
$$
$$
x = \frac{21.250.000}{85} = 250.000
$$
### 👉 **Kết quả:**
* Váy: **250.000 đồng/cái**
* Quần: **750.000 đồng/cái**
---
## ✅ **Câu 2: Ô tô và xe máy**
**Đề bài:**
* A và B cách nhau 180 km
* Gặp nhau sau 2 giờ, đi **ngược chiều**
* Ô tô nhanh hơn xe máy **10 km/h**
### 👣 **Bước 1: Đặt ẩn**
* Gọi vận tốc xe máy: **x (km/h)**
→ Vận tốc ô tô: **x + 10**
Vì 2 xe đi ngược chiều, tổng quãng đường = tổng quãng đường 2 xe đi trong 2h:
$$
2x + 2(x + 10) = 180
\Rightarrow 2x + 2x + 20 = 180
\Rightarrow 4x = 160
\Rightarrow x = 40
$$
### 👉 **Kết quả:**
* Xe máy: **40 km/h**
* Ô tô: **50 km/h**
---
## ✅ **Câu 3: Ca nô và dòng nước**
**Đề bài:**
* Đi 108 km xuôi dòng + 63 km ngược dòng hết **7h**
* Đi 81 km xuôi dòng + 84 km ngược dòng cũng **7h**
### 👣 **Bước 1: Đặt ẩn**
* Gọi vận tốc ca nô (khi nước yên lặng): **x km/h**
* Gọi vận tốc dòng nước: **y km/h**
→ Vận tốc xuôi dòng: **x + y**, ngược dòng: **x - y**
---
### 👣 **Lập 2 phương trình theo thời gian:**
**Phương trình 1 (tổng thời gian = 7):**
$$
\frac{108}{x + y} + \frac{63}{x - y} = 7 \tag{1}
$$
**Phương trình 2:**
$$
\frac{81}{x + y} + \frac{84}{x - y} = 7 \tag{2}
$$
---
### 👣 **Giải hệ phương trình**
Trừ (2) cho (1):
$$
\left(\frac{81 - 108}{x + y}\right) + \left(\frac{84 - 63}{x - y}\right) = 0
\Rightarrow \frac{-27}{x + y} + \frac{21}{x - y} = 0
$$
→ Giải:
$$
\frac{21}{x - y} = \frac{27}{x + y}
\Rightarrow 21(x + y) = 27(x - y)
\Rightarrow 21x + 21y = 27x - 27y
\Rightarrow 6x = 48y
\Rightarrow x = 8y \tag{3}
$$
---
Thế (3) vào (1):
$$
\frac{108}{8y + y} + \frac{63}{8y - y} = 7
\Rightarrow \frac{108}{9y} + \frac{63}{7y} = 7
\Rightarrow \frac{12}{y} + \frac{9}{y} = 7
\Rightarrow \frac{21}{y} = 7
\Rightarrow y = 3
\Rightarrow x = 24
$$
### 👉 **Kết quả:**
* Ca nô: **24 km/h**
* Dòng nước: **3 km/h**
---
## ✅ **Câu 4: Ô tô đi từ A đến B**
**Đề bài:**
* Quãng đường từ A đến B, dự định đến **12h trưa**
* Nếu chạy 35 km/h → **chậm 2 giờ**
* Nếu chạy 50 km/h → **sớm 1 giờ**
### 👣 **Bước 1: Đặt ẩn**
* Gọi quãng đường AB là **x (km)**
Với vận tốc 35:
$$
\text{Thời gian đi} = \frac{x}{35} = t_1
\Rightarrow t_1 = \text{thời gian dự định} + 2
$$
Với vận tốc 50:
$$
\frac{x}{50} = \text{thời gian dự định} - 1
$$
---
### 👣 **Lập phương trình**
Từ 2 biểu thức trên:
$$
\frac{x}{35} = \frac{x}{50} + 3
$$
Giải:
$$
\frac{x}{35} - \frac{x}{50} = 3
\Rightarrow x \left( \frac{1}{35} - \frac{1}{50} \right) = 3
\Rightarrow x \cdot \left( \frac{50 - 35}{1750} \right) = 3
\Rightarrow x \cdot \frac{15}{1750} = 3
\Rightarrow x = \frac{3 \cdot 1750}{15} = 350
$$
→ Quãng đường AB = **350 km**
---
### 👣 **Tìm thời gian xuất phát**
* Với vận tốc 50:
$$
\text{Thời gian đi} = \frac{350}{50} = 7 \text{ giờ}
$$
→ Vì đến sớm 1 giờ, nên thời gian dự định đi là **8 giờ**
→ Xuất phát lúc:
$$
12h - 8h = \boxed{4 giờ sáng}
$$
---
## ✅ **Tóm tắt đáp án cuối cùng:**
| Câu | Kết quả |
| --- | --------------------------------------------- |
| 1 | Váy: 250.000 đồng, Quần: 750.000 đồng |
| 2 | Xe máy: 40 km/h, Ô tô: 50 km/h |
| 3 | Ca nô: 24 km/h, Dòng nước: 3 km/h |
| 4 | Quãng đường AB: 350 km, Xuất phát lúc 4h sáng |
Nếu bạn cần mình vẽ sơ đồ, bảng, hoặc giải thích thêm cách lập phương trình, cứ nói nhé!
Tk
Hok tốt:3
Câu 1:
Đề bài:
Mua 10 cái váy và 25 cái quần hết 21.250.000 đồng, biết mua 3 cái váy thì bằng tiền 1 cái quần. Tìm số tiền mua váy và mua quần.
Gọi:
Theo đề bài:
Thay vào phương trình đầu:
\(10 x + 25 y = 21.250.000 \Rightarrow 10 \cdot \frac{y}{3} + 25 y = 21.250.000 \Rightarrow \frac{10 y}{3} + 25 y = 21.250.000 \Rightarrow \frac{10 y + 75 y}{3} = 21.250.000 \Rightarrow \frac{85 y}{3} = 21.250.000 \Rightarrow y = \frac{21.250.000 \cdot 3}{85} = 750.000\)
⟹ \(y = 750.000\) đồng (giá 1 cái quần)
⟹ \(x = \frac{y}{3} = 250.000\) đồng (giá 1 cái váy)
Kết luận:
Câu 2:
Đề bài:
Ô tô và xe máy đi ngược chiều từ 2 điểm cách nhau 180 km, gặp nhau sau 2 giờ. Vận tốc ô tô lớn hơn xe máy 10 km/h. Tìm vận tốc mỗi xe.
Gọi:
Do đi ngược chiều, sau 2 giờ gặp nhau, tổng quãng đường là 180 km:
\(\left(\right. x + x + 10 \left.\right) \cdot 2 = 180 \Rightarrow \left(\right. 2 x + 10 \left.\right) \cdot 2 = 180 \Rightarrow 2 x + 10 = 90 \Rightarrow 2 x = 80 \Rightarrow x = 40\)
⟹ Xe máy: 40 km/h
⟹ Ô tô: 50 km/h
Câu 3:
Đề bài:
Ca nô đi 108 km xuôi dòng + 63 km ngược dòng mất 7 giờ.
Một ngày khác, đi 81 km xuôi dòng + 84 km ngược dòng cũng mất 7 giờ.
Tìm vận tốc ca nô (khi nước yên lặng) và vận tốc dòng nước.
Gọi:
⟹ Xuôi dòng: \(x + y\)
⟹ Ngược dòng: \(x - y\)
Ta có hệ phương trình:
Giải hệ: Trừ vế cho vế:
\(\left(\right. \frac{108}{x + y} - \frac{81}{x + y} \left.\right) + \left(\right. \frac{63}{x - y} - \frac{84}{x - y} \left.\right) = 0 \Rightarrow \frac{27}{x + y} - \frac{21}{x - y} = 0 \Rightarrow \frac{27}{x + y} = \frac{21}{x - y}\)
Nhân chéo:
\(27 \left(\right. x - y \left.\right) = 21 \left(\right. x + y \left.\right) \Rightarrow 27 x - 27 y = 21 x + 21 y \Rightarrow 6 x = 48 y \Rightarrow x = 8 y\)
Thay vào phương trình (1):
\(\frac{108}{x + y} + \frac{63}{x - y} = 7 \Rightarrow \frac{108}{8 y + y} + \frac{63}{8 y - y} = 7 \Rightarrow \frac{108}{9 y} + \frac{63}{7 y} = 7 \Rightarrow \frac{12}{y} + \frac{9}{y} = 7 \Rightarrow \frac{21}{y} = 7 \Rightarrow y = 3\)
⟹ \(x = 8 y = 24\)
Kết luận:
Câu 4:
Đề bài:
Ô tô dự định đến B lúc 12h trưa.
Tính quãng đường AB và thời gian xuất phát.
Gọi:
⟹ \(x = 35 \left(\right. t + 2 \left.\right)\)
⟹ \(x = 50 \left(\right. t - 1 \left.\right)\)
Lập hệ:
\(35 \left(\right. t + 2 \left.\right) = 50 \left(\right. t - 1 \left.\right) \Rightarrow 35 t + 70 = 50 t - 50 \Rightarrow 15 t = 120 \Rightarrow t = 8\)
⟹ Quãng đường: \(x = 35 \left(\right. t + 2 \left.\right) = 35 \cdot 10 = 350\) km
⟹ Thời gian dự định đi là 8 giờ ⟹ xuất phát lúc:
\(12 h - 8 h = 4 h s \overset{ˊ}{a} n g\)
Kết luận: