Công suất, vận tốc tối đa và hệ thống treo lốp của Honda Civic Fl5 type R

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

VA

Vũ Anh Khôi

11 giờ trước (16:23) - olm

Công suất, vận tốc tối đa và hệ thống treo lốp của Honda Civic Fl5 type R

#Hỏi cộng đồng OLM #Vật lý lớp 12

1

TD

Tôi đã bị lãng quên...

11 giờ trước (16:29)

Thông tin chính về Honda Civic F15 Type R:

Công suất: Đề cập đến sức mạnh động cơ của xe.
Vận tốc tối đa: Chỉ ra tốc độ cao nhất mà xe có thể đạt được.
Hệ thống treo lốp: Mô tả cấu trúc và công nghệ treo của xe, ảnh hưởng đến khả năng vận hành và sự thoải mái.

Các câu hỏi dưới đây có thể giống với câu hỏi trên

NN

nhung nguyen

16 tháng 2 2017

hai máy kéo nhỏ :
1 xe có công suất là 2kw
vận tốc tối đa là 20km/h
xe kia có công suất là 4kw
vận tốc tối đa là 40km/h
tìm vận tốc tối đa của 2 xe khi chúng được nối nhau

lý 10

#Hỏi cộng đồng OLM #Vật lý lớp 12

0

MT

Mai Trần

1 tháng 6 2016

Một động cơ điện xoay chiều một pha hoạt động bình thường với điện áp hiệu dụng bằng 220V và dòng điện hiệu dụng bằng 1A. Biết điện trở trong của động cơ là r =35,2\(\Omega\) và hệ số công suất của động cơ là 0,8. Hiệu suất của động cơ (tỉ số giữa công suất hữu ích và công suất tiêu thụ toàn phần) bằng A. 91%....

#Hỏi cộng đồng OLM #Vật lý lớp 12

1

SS

Sky SơnTùng

1 tháng 6 2016

\(H=\frac{P_{coich}}{P}=1-\frac{P_{hp}}{P}=1-\frac{rI^2}{UI\cos}=80\%\)

Đáp án D

TN

Thy Nguyễn

20 tháng 8 2016

Nối hai cực của một máy phát điện xoay chiều vào hai đầu đoạn mạch RLC .Bỏ qua điện trở dây nối ,coi từ thông cực đại gửi qua các cuộn dây của máy phát không đổi.Khi máy phát quay với tốc độ n vòng /phút thì công suất tiêu thụ là P,hệ số công suất là 1/√2.Khi máy phát quay với tốc độ 2n(vòng/phút)thì công suất tiêu thụ điện là 4P.Khi máy phát quay với tốc độ √2n vòng/phút...

#Hỏi cộng đồng OLM #Vật lý lớp 12

2

TH

Trần Hoàng Sơn

20 tháng 8 2016

Ta có:

\(P=\dfrac{U_{1}^{2}}{Z_{1}^{2}}R\)

\(4P=\dfrac{U_{2}^{2}}{Z_{2}^{2}}R\)

\(\Rightarrow \dfrac{P}{4P}=\left( \dfrac{U_{1}}{U_{2}} \right)^{2}\left( \dfrac{Z_{2}}{Z_{1}} \right)^{2}\)

\(\Leftrightarrow \dfrac{1}{4}=\left(\dfrac{n_{1}}{n_{2}} \right)^{2}\left(\dfrac{Z_{2}}{Z_{1}} \right)^{2}\rightarrow Z_{2}=Z_{1}\)

Ta nghĩ đến bài toán f biến thiên có 2 giá trị của f mạch cho cùng 1 tổng trở.\(\Rightarrow n_{0}=\sqrt{n_{1}n_{2}}=\sqrt{2}n \)

Vậy khi roto quay với tốc độ \(\sqrt{2}n\) mạch xảy ra cộng hưởng.

Công suất: \(P_0=\dfrac{U_{0}^{2}}{R}\)

Lại có:

\(P=\dfrac{U_{1}^{2}}{Z_{1}^{2}}R=\dfrac{U_{1}^{2}}{2R^{2}}R=\dfrac{U_{1}^{2}}{2R}\) (Do \(Z_1=\sqrt 2.R\))

\(\Rightarrow \dfrac{P}{P_{0}}=\dfrac{U_{1}^{2}}{2U_{0}^{2}}=\dfrac{1}{2}\left(\dfrac{n_{1}}{n_{0}} \right)^{2}=\dfrac{1}{4} \Rightarrow P_{0}=4P\)

Vậy: \(P_0=4P\)

LN

Lê Nguyên Hạo

20 tháng 8 2016

\(U_0=\omega\phi\)

\(P=I^2R=\left(\frac{U_0}{Z\sqrt{2}}\right)^2R=\frac{\omega^2\phi^2R}{2\left(R^2\left(\omega L-\frac{1}{\omega c}\right)^2\right)}\)

\(=\frac{\phi^2R}{2\left(\frac{R^2}{\omega^2}+\left(L-\frac{1}{\omega^2c}\right)^2\right)}=\frac{\phi^2R}{2\left(\frac{1}{\omega^4C^2}+\frac{R^2-2L}{\omega^2}+L^2\right)}\)

Do đó: \(\phi\) không đổi. Đặt : \(\frac{1}{\omega^2}=x\)

Xét f (x) \(=\frac{x^2}{C^2}+\left(R^2-2L\right)x+2L^2\)

=> P_max \(\Leftrightarrow x_0=\frac{2L-R^2}{2C^2}\)

Do P phụ thuộc hàm bậc 2 nên

\(P_1=P_2\Rightarrow x_1+x_2=2x_0\Leftrightarrow\frac{1}{\omega^2_1}+\frac{1}{\omega^2_2}=\frac{2}{\omega^2_0}\)

Mặt khác, tốc độ quay của rôto tỉ lệ thuận với tần số góc nên

\(\frac{1}{n^2_1}+\frac{1}{n^2_2}+\frac{1}{n^2_0}\Leftrightarrow n_0=2\frac{n^2_1n^2_2}{n^2_1+n^2_2}\)

HD

Hoàng Đức Long

14 tháng 9 2017

Điện năng truyền tải từ trạm điện đến nơi tiêu thụ bằng một hệ thống đường dây nhất định. Gọi P, ΔP và Ptt lần lượt là công suất đưa lên đường dây, công suất hao phí trên đường dây và công suất nơi tiêu thụ nhận được. Hiệu suất truyền tải điện trên hệ thống đường dây đó là A. ΔP/P. B. Ptt/P. C. ΔP/Ptt. D. P/Ptt....

#Hỏi cộng đồng OLM #Vật lý lớp 12

1

VT

Vũ Thành Nam

14 tháng 9 2017

+ Hiệu suất truyền tải điện năng được tính là: H=Ptt/P .

Đáp án B

NM

nguyễn minh

21 tháng 6 2016

Đặt vào hai đầu đoạn mạch RLC nối tiếp một điện áp xoay chiều có giá trị hiệu dụng không đổi và tần số thay đổi được. Khi tần số là f1 thì hệ số công suất của đoạn mạch bằng 0,4 và công suất tiêu thụ của nó bằng 160W. Khi tần số là f2 thì công suất tiêu thụ của đoạn mạch bằng 360W. Hệ số công suất của mạch khi đó...

#Hỏi cộng đồng OLM #Vật lý lớp 12

2

TH

Trần Hoàng Sơn

21 tháng 6 2016

Áp dụng: \(P=\dfrac{U^2}{R}\cos^2\varphi\)

\(\Rightarrow 160=\dfrac{U^2}{R}.0,4^2\) (1)

\(340=\dfrac{U^2}{R}.\cos^2\varphi\) (2)

Lấy (1) chia (2) vế với vế ta tìm đc \(\cos\varphi = 0,6\)

TA

Trương Anh Tài

21 tháng 6 2016

\(P_1=UI.cos\varphi=\frac{U^2.R}{Z.R}.cos\varphi=\frac{U^2}{R}.cos\varphi^2_1\)

\(P_2=UI.cos\varphi=\frac{U^2.R}{Z.R}.cos\varphi=\frac{U^2}{R}.cos\varphi^2_2\)

\(cos\varphi_2=0,6\)

đáp án B

TN

thu nguyen

6 tháng 7 2016

Một thang máy và tải của nó có khối lượng toàn phần 1600kg. Tím sức căng của dây cáp treo nó khi nó đi xuống với vận tốc 12m/s thì hãm với vận tốc không đổi và dừng lại sau đoạn đường 42m.

#Hỏi cộng đồng OLM #Vật lý lớp 12

1

DT

Đặng Thị Cẩm Tú

9 tháng 7 2016

Khi thang máy đi lên lực căng của dây cáp treo thang máy là:
          T=(m1+m2)(g+a)(1)
và lực ép của người lên mặt sàn thang máy có độ lớn:
          N=m2(g+a)
a) Trường hợp thang máy đi lên. Chọn chiều dương là chiều chuyển động. Dựa vào đồ thị ta nhận thấy:
- Ứng với đoạn OA trên đồ thị, thang máy chuyển động nhanh dần đều với gia tốc
          a1=52=2,5m/s2
Theo (1) lực căng của dây cáp bằng:
         T1=(m1+m2)(g+a1)=6250N
Theo (2) lực ép của người lên mặt sàn thang máy bằng:
         N1=m2(g+a)=625N
- Ứng với đoạn AB thăng máy chuyển động thẳng đều (a=0) lực căng của dây cáp là: T2=(m1+m2)g=5000N
và lực éo của người lên mặt sàn thang máy bằng:
          N2=m2g=500N
- Ứng với đoạn BC trên đồ thị, thang máy chuyển động chậm dần đều với gia tốc
          a2=−52=−2,5m/s2
Lực căng của dây cáp là: T3=(m1+m2)(g+a2)=3750N
Lực ép của người lên mặt sàn là: N3=m2

HD

Hoàng Đức Long

4 tháng 6 2018

Một lò xo độ cứng k=50 N/m, một đầu cố định, đầu còn lại treo vật nặng khối lượng m=100g. Điểm treo lò xo chịu được lực tối đa không quá 4N. Lấy g=10m/s2. Để hệ thống không bị rơi thì vật nặng dao động theo phương thẳng đứng với biên độ không quá A. 10 cm. B. 5 cm. C. 8 cm. D. 6 cm....

#Hỏi cộng đồng OLM #Vật lý lớp 12

1

VT

Vũ Thành Nam

4 tháng 6 2018

Giải thích: Đáp án D

Phương pháp: Sử dụng lý thuyết về dao động điều hòa của CLLX

Cách giải:

+ Tần số góc: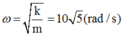

Độ giãn của lò xo ở VTCB:

+ Điểm treo của con lắc chịu được lực tối đa không quá 4N => F_đhmax ≤ 4N

HD

Hoàng Đức Long

25 tháng 9 2017

Một lò xo độ cứng k = 50 N/m, một đầu cố định, đầu còn lại có treo vật nặng khối lượng m = 100 g. Điểm treo lò xo chịu được lực tối đa không quá 4 N. Lấy g = 10 m/s2. Để hệ thống không bị rơi thì vật nặng dao động theo phương thẳng đứng với biên độ không quá A. 10 cm. B. 6 cm . C.5 cm. D. 8 cm ....

#Hỏi cộng đồng OLM #Vật lý lớp 12

1

VT

Vũ Thành Nam

25 tháng 9 2017

DD

Đăng Duy Nguyễn

17 tháng 5 2016

Câu hỏi hay

Động cơ điện xoay chiều hoạt động bình thường ở điện áp hiệu dụng 220V thì sinh công suất cơ học là 80W . Biết dộng cơ có hệ số công suất là 0,8 , điện trở thuần của dây quấn là 32 Ω và hiệu suất > 85% . Công suất hao phí chủ yếu do toả nhiệt. Cường độ dòng điện cực đại qua động cơ là

#Hỏi cộng đồng OLM #Vật lý lớp 12

1

HY

Hai Yen

17 tháng 5 2016

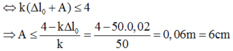
\(P=UI\cos\varphi\)

=> \(I=\frac{P}{U\cos\varphi}=\frac{P_i+I^2r}{U\cos\varphi}=\frac{80+I^2.32}{220.0.8}\)

=> phương trình bậc 2 của I và bấm máy tính

\(I_1=5\)(loại vì hiệu suất \(H=\frac{80}{UI\cos\varphi}=9,09\%\))

hoặc \(I_2=0.5\) (chọn)

=> \(I_0=I\sqrt{2}=0,5\sqrt{2}A.\)

chọn đáp án D.