Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C H D 1 2
Ta có: ^ABC=^HAC (Cùng phụ với ^BAH) => ^HAC=650 hay ^HAD=650.
^H1=^H2=^AHC/2=450
=> ^ADH=1800-(^HAD+^H1)=1800-1100=700.
Vậy ^ADH=700.

ΔABC vuông tại A
=>\(\hat{B}+\hat{C}=90^0\)
mà \(\hat{B}-\hat{C}=\alpha\)
nên \(\hat{B}=\frac{90^0+\alpha}{2}\)
AD là phân giác của góc BAC
=>\(\hat{BAD}=\hat{CAD}=\frac{90^0}{2}=45^0\)
Ta có: \(\hat{BAH}+\hat{B}=90^0\)
=>\(\hat{BAH}=90^0-\hat{B}=90^0-\frac{90^0+\alpha}{2}=\frac{90^0-\alpha}{2}=45^0-\frac12\cdot\alpha\)
Vì \(\hat{BAH}<\hat{BAD}\)
nên tia AH nằm giữa hai tia AB và AD
=>\(\hat{BAH}+\hat{HAD}=\hat{BAD}\)
=>\(\hat{HAD}=45^0-\left(45^0-\frac12\cdot\alpha\right)=\frac12\cdot\alpha\)

a, Ta có:
Góc A + góc B + góc C = 180o
=> Góc C = 180o - ( góc A + góc B)
=> Góc C = 180o - ( 90o + 60o)
=> Góc C = 30o
b, Vì AD là tia phân giác góc A
Mà góc A = 90o (giả thiết)
=> Góc BAD = DAC = 90o : 2 = 45o
Ta có: Góc BAD + góc ABD + góc ADB = 180o
=> 45o + 60o + góc ADB = 180o
=> góc ADB = 75o
c, Ta có: góc AHD + góc HDA + góc DAH = 180o
=> góc DAH = 180o - 90o - 75o
=> góc DAH = 15o

Bài làm
a) Xét tam ABC vuông tại A có:
\(\widehat{ACB}+\widehat{ABC}=90^0\)( hai góc phụ nhau )
hay \(\widehat{ACB}+60^0=90^0\)
=> \(\widehat{ACB}=90^0-60^0=30^0\)
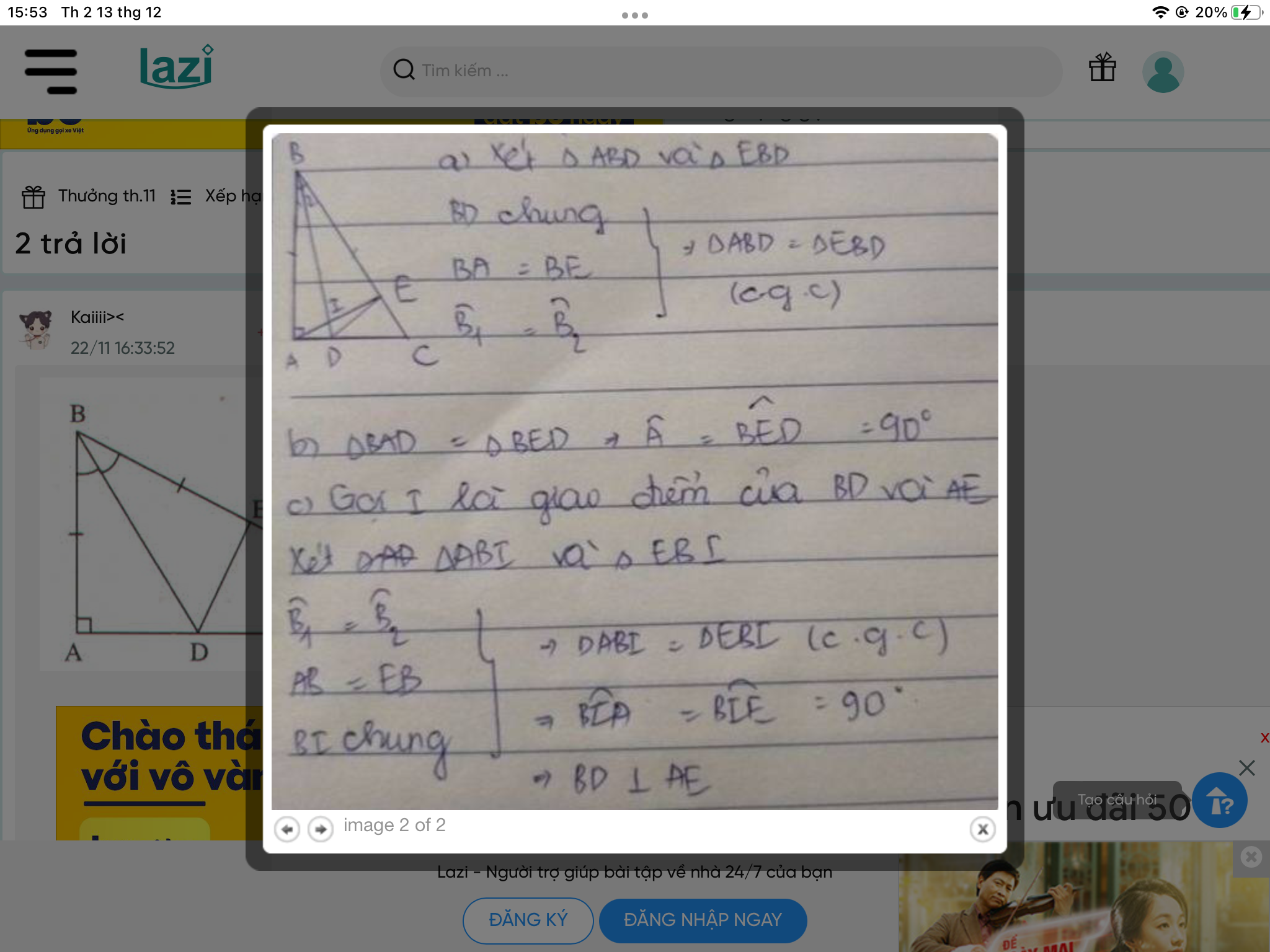
b) Xét tam giác ABE và tam giác DBE có:
\(\widehat{BAE}=\widehat{BDE}=90^0\)
Cạnh huyền: BE chung
Cạnh góc vuông: AB = BD ( gt )
=> Tam giác ABE = tam giác DBE ( cạnh huyền - cạnh góc vuông )
=> \(\widehat{ABE}=\widehat{DBE}\)( hai góc tương ứng )
=> BI là tia phân giác của góc BAC
Mà I thược BE
=> BE là tia phân giác của góc BAC
Gọi I là giao điểm BE và AD
Xét tam giác AIB và tam giác DIB có:
AB = BD ( gt )
\(\widehat{ABE}=\widehat{DBE}\)( cmt )
BI chung
=> Tam giác AIB = tam giác DIB ( c.g.c )
=> AI = ID (1)
=> \(\widehat{BIA}=\widehat{BID}\)
Ta có: \(\widehat{BIA}+\widehat{BID}=180^0\)( hai góc kề bù )
Hay \(\widehat{BIA}=\widehat{BID}=\frac{180^0}{2}=90^0\)
=> BI vuông góc với AD tại I (2)
Từ (1) và (2) => BI là đường trung trực của đoạn AD
Mà I thược BE
=> BE là đường trung trực của đoạn AD ( đpcm )
c) Vì tam giác ABE = tam giác DBE ( cmt )
=> AE = ED ( hai cạnh tương ứng )
Xét tam giác AEF và tam giác DEC có:
\(\widehat{EAF}=\widehat{EDC}=90^0\)
AE = ED ( cmt )
\(\widehat{AEF}=\widehat{DEF}\)( hai góc đối )
=> Tam giác AEF = tam giác DEC ( g.c.g )
=> AF = DC
Ta có: AF + AB = BF
DC + BD = BC
Mà AF = DC ( cmt )
AB = BD ( gt )
=> BF = BC
=> Tam giác BFC cân tại B
=> \(\widehat{BFC}=\widehat{BCF}=\frac{180^0-\widehat{FBC}}{2}\) (3)
Vì tam giác BAD cân tại B ( cmt )
=> \(\widehat{BAD}=\widehat{BDA}=\frac{180^0-\widehat{FBC}}{2}\) (4)
Từ (3) và (4) => \(\widehat{BAD}=\widehat{BFC}\)
Mà Hai góc này ở vị trí đồng vị
=> AD // FC
d) Xét tam giác ABC vuông tại A có:
\(\widehat{ACB}+\widehat{ABC}=90^0\)( hai góc phụ nhau ) (5)
Xét tam giác DEC vuông tại D có:
\(\widehat{DEC}+\widehat{ACB}=90^0\)( hai góc phụ nhau ) (6)
Từ (5) và (6) => \(\widehat{ABC}=\widehat{DEC}\)
Ta lại có:
\(\widehat{ABC}>\widehat{EBC}\)
=> AC > EC
Mà \(\widehat{EBC}=\frac{1}{2}\widehat{ABC}\)
=> EC = 1/2 AC.
=> E là trung điểm AC
Mà EC = EF ( do tam giác AEF = tam giác EDC )
=> EF = 1/2AC
=> AE = EC = EF
Và AE = ED ( cmt )
=> ED = EC
Mà EC = 1/2AC ( cmt )
=> ED = 1/2AC
=> 2ED = AC ( đpcm )
Mình chứng minh ra kiểu này cơ. không biết đề đúng hay sai!??
Búng luôn rồi !
Ta có: ΔABC vuông tại A
=>\(\hat{ABC}+\hat{ACB}=90^0\)
=>\(\hat{ACB}=90^0-65^0=25^0\)
ΔHAC vuông tại H
=>\(\hat{HAC}+\hat{HCA}=90^0\)
=>\(\hat{HAC}=90^0-25^0=65^0\)
HD là phân giác của góc AHC
=>\(\hat{AHD}=\hat{CHD}=\frac12\cdot\hat{AHC}=45^0\)
Xét ΔCDH có \(\hat{ADH}\) là góc ngoài tại đỉnh D
nên \(\hat{ADH}=\hat{DCH}+\hat{DHC}=25^0+45^0=70^0\)