K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

8 tháng 9 2023
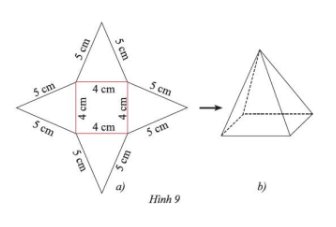
Sau khi thực hiện theo hướng dẫn, ta được sản phẩm như Hình 9b.

21 tháng 2 2022
Bài 1:
Xét ΔABC có
M là trung điểm của BC
ME//AC
Do đó: E là trung điểm của AB
Xét ΔABC có
M là trung điểm của BC
MF//AB
DO đó: F là trung điểm của AC
Xét ΔABC có
E là trung điểm của AB
F là trung điểm của AC
Do đó: EF là đường trung bình
=>EF//BC
hay BEFC là hình thang
mà \(\widehat{B}=\widehat{C}\)
nên BEFC là hình thang cân
Phân tích:
Sau khi cắt 4 góc hình vuông cạnh \(x\), ta gập các mép lên để tạo hộp.
\(12 - 2 x \left(\right. c m \left.\right)\)
\(x \left(\right. c m \left.\right)\)
Thể tích hộp \(V\):
\(V = \text{chi} \overset{ˋ}{\hat{\text{e}}} \text{u}\&\text{nbsp};\text{d} \overset{ˋ}{\text{a}} \text{i} \times \text{chi} \overset{ˋ}{\hat{\text{e}}} \text{u}\&\text{nbsp};\text{r}ộ\text{ng} \times \text{chi} \overset{ˋ}{\hat{\text{e}}} \text{u}\&\text{nbsp};\text{cao} = \left(\right. 12 - 2 x \left.\right) \left(\right. 12 - 2 x \left.\right) \left(\right. x \left.\right) = x \left(\right. 12 - 2 x \left.\right)^{2}\)
Bước 1: Viết biểu thức thể tích:
\(V = x \left(\right. 12 - 2 x \left.\right)^{2}\)
Mở rộng:
\(V = x \left(\right. 144 - 48 x + 4 x^{2} \left.\right) = 144 x - 48 x^{2} + 4 x^{3}\)
Bước 2: Tìm cực trị (cực đại):
Tính đạo hàm \(V^{'} \left(\right. x \left.\right)\):
\(V^{'} \left(\right. x \left.\right) = 144 - 96 x + 12 x^{2}\)
Đặt \(V^{'} \left(\right. x \left.\right) = 0\) để tìm nghiệm:
\(12 x^{2} - 96 x + 144 = 0\)
Chia cả phương trình cho 12:
\(x^{2} - 8 x + 12 = 0\)
Bước 3: Giải phương trình bậc hai:
\(x = \frac{8 \pm \sqrt{64 - 48}}{2} = \frac{8 \pm \sqrt{16}}{2} = \frac{8 \pm 4}{2}\)
Hai nghiệm:
Bước 4: Xét miền nghiệm hợp lệ
Bước 5: Kiểm tra giá trị thể tích tại \(x = 2\) và \(x = 6\):
Bước 6: Kiểm tra giới hạn khi \(x \rightarrow 0\):
\(V \left(\right. 0 \left.\right) = 0\)
Kết luận:
Thể tích lớn nhất tại \(x = 2\) cm.
@ Phong, nếu bạn chép mạng thì vui lòng ghi thêm chữ "tham khảo" ở phần đầu bài nhé!