Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
I don't now
or no I don't
..................
sorry
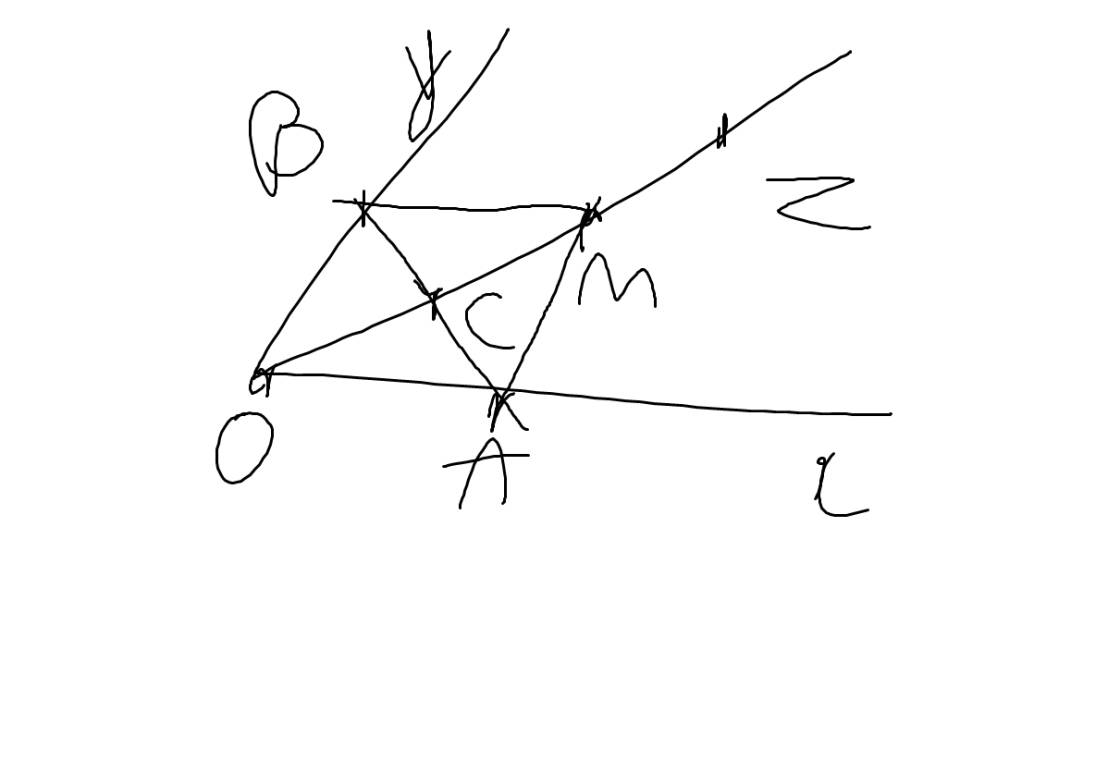
a: ΔOAB cân tại O
mà OC là phân giác
nên OC vuông góc AB và C là trung điểm của AB
b: Xét tứ giác OAMB có
C là trung điểm chung của OM và AB
=>OAMB là hình bình hành
=>OA//MB và OB//MA
a: Xét ΔOAC và ΔOBC có
OA=OB
\(\widehat{AOC}=\widehat{BOC}\)
OC chung
Do đó: ΔOAC=ΔOBC
=>AC=BC
=>C là trung điểm của AB
Ta có: CA=CB
=>C nằm trên đường trung trực của AB(1)
ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra OC là đường trung trực của AB
=>CO\(\perp\)AB
b: Xét ΔOAC và ΔMBC có
CO=CM
\(\widehat{OCA}=\widehat{MCB}=90^0\)
CA=CB
Do đó: ΔOAC=ΔMBC
=>\(\widehat{OAC}=\widehat{MBC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên OA//BM
Xét ΔCBO vuông tại C và ΔCAM vuông tại C có
CB=CA
CO=CM
Do đó: ΔCBO=ΔCAM
=>\(\widehat{CBO}=\widehat{CAM}\)
mà hai góc này là hai góc ở vị trí so le trong
nên BO//AM
Mình nghĩ khó mà có người giải hết chỗ bài tập đấy của bạn, nhiều quá
3/ (Bạn tự vẽ hình giùm)
a/ \(\Delta ABC\)và \(\Delta ADC\)có:
\(\widehat{BAC}=\widehat{ACD}\)(AB // DC; ở vị trí so le trong)
Cạnh AC chung
\(\widehat{CAD}=\widehat{ACB}\)(AB // DC; ở vị trí so le trong)
=> \(\Delta ABC\)= \(\Delta ADC\)(g. c. g)
=> AD = BC (hai cạnh tương ứng)
và AB = DC (hai cạnh tương ứng)
b/ Ta có AD = BC (cm câu a)
và \(AN=\frac{1}{2}AD\)(N là trung điểm AD)
và \(MC=\frac{1}{2}BC\)(M là trung điểm BC)
=> AN = MC
Chứng minh tương tự, ta cũng có: BM = ND
\(\Delta AMB\)và \(\Delta CND\)có:
BM = ND (cmt)
\(\widehat{ABM}=\widehat{NDC}\)(AB // CD; ở vị trí so le trong)
AB = CD (\(\Delta ABC\)= \(\Delta ADC\))
=> \(\Delta AMB\)= \(\Delta CND\)(c. g. c)
=> \(\widehat{BAM}=\widehat{NCD}\)(hai góc tương ứng)
và \(\widehat{BAC}=\widehat{ACN}\)(\(\Delta ABC\)= \(\Delta ADC\))
=> \(\widehat{BAC}-\widehat{BAM}=\widehat{ACN}-\widehat{NCD}\)
=> \(\widehat{MAC}=\widehat{ACN}\)(1)
Chứng minh tương tự, ta cũng có \(\widehat{AMC}=\widehat{ANC}\)(2)
và AN = MC (cmt) (3)
=> \(\Delta MAC=\Delta NAC\)(g, c. g)
=> AM = CN (hai cạnh tương ứng) (đpcm)
c/ \(\Delta AOB\)và \(\Delta COD\)có:
\(\widehat{BAO}=\widehat{OCD}\)(AB // DC; ở vị trí so le trong)
AB = CD (cm câu a)
\(\widehat{ABO}=\widehat{ODC}\)(AD // BC; ở vị trí so le trong)
=> \(\Delta AOB\)= \(\Delta COD\)(g. c. g)
=> OA = OC (hai cạnh tương ứng)
và OB = OD (hai cạnh tương ứng)
d/ \(\Delta ONA\)và \(\Delta MOC\)có:
\(\widehat{AON}=\widehat{MOC}\)(đối đỉnh)
OA = OC (O là trung điểm AC)
\(\widehat{OAN}=\widehat{OCM}\)(AM // NC; ở vị trí so le trong)
=> \(\Delta ONA\)= \(\Delta MOC\)(g. c. g)
=> ON = OM (hai cạnh tương ứng)
=> O là trung điểm MN
=> M, O, N thẳng hàng (đpcm)
Để chứng minh ba điểm O,N,M thẳng hàng, ta sẽ chứng minh tia OM và tia ON trùng nhau.
Ta đã có các điều kiện từ các phần trước:
Chứng minh △OMI=△OMK.
Vậy △OMI=△OMK (cạnh huyền - cạnh góc vuông).
Chứng minh △OAK=△OBI.
Vậy △OAK=△OBI (cạnh huyền - cạnh góc vuông).
Chứng minh O,N,M thẳng hàng.
Vậy △OAN=△OBN (c.g.c).
Từ đó, ∠AON=∠BON, suy ra ON là tia phân giác của ∠AOB hay ∠xOy.
Mặt khác, ta cũng có OM là tia phân giác của ∠xOy (từ △OMI=△OMK suy ra ∠MOI=∠MOK, tức là OM là tia phân giác).
Vì cả hai tia ON và OM đều là tia phân giác của cùng một góc ∠xOy, nên hai tia này phải trùng nhau.
suy ra Ba điểm O,N,M thẳng hàng.
a: Xét ΔOCA và ΔOCB có
OC chung
\(\hat{COA}=\hat{COB}\)
OA=OB
Do đó: ΔOCA=ΔOCB
=>CA=CB
=>C là trung điểm của AB
ΔOCA=ΔOCB
=>\(\hat{OCA}=\hat{OCB}\)
mà \(\hat{OCA}+\hat{OCB}=180^0\) (hai góc kề bù)
nên \(\hat{OCA}=\hat{OCB}=\frac{180^0}{2}=90^0\)
=>OC⊥AB tại C
b: Xét ΔCAM vuông tại C và ΔCBO vuông tại C có
CA=CB
CM=CO
Do đó: ΔCAM=ΔCBO
=>\(\hat{CAM}=\hat{CBO}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AM//BO
Xét ΔCBM vuông tại C và ΔCAO vuông tại C có
CB=CA
CM=CO
Do đó: ΔCBM=ΔCAO
=>\(\hat{CBM}=\hat{CAO}\)
mà hai góc này là hai góc ở vị trí so le trong
nên OA//BM
c: Xét ΔOKM vuông tại K và ΔOIM vuông tại I có
OM chung
\(\hat{KOM}=\hat{IOM}\)
Do đó: ΔOKM=ΔOIM
=>OK=OI
ta có: OK=OA+AK
OI=OB+BI
mà OK=OI và OA=OB
nên AK=BI
d: Xét ΔAKI và ΔBIK có
AK=BI
KI chung
AI=BK
Do đóΔAKI=ΔBIK
=>\(\hat{AIK}=\hat{BKI}\)
=>\(\hat{NIK}=\hat{NKI}\)
=>NK=NI
=>N nằm trên đường trung trực của KI(1)
ta có: OK=OI
=>O nằm trên đường trung trực của KI(2)
Ta có: ΔOKM=ΔOIM
=>MK=MI
=>M nằm trên đường trung trực của KI(3)
Từ (1),(2),(3) suy ra O,N,M thẳng hàng