Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi giao điểm của HF và AC là I
Giao điểm của HE và AB là K
Ta có PHK+NHI=90-PKH+90-NIH=180-(180-PAN)=PAN (1)
Mà tứ giác APNH là tứ giác nội tiếp( do 2 góc đối cộng lại =180)
=>PAN+PHN=180 (2)
Thay (1) vào (2) ta đươck PHK+PHN+NHI=180
hay E,H,F thẳng hàng

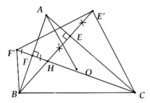
a, ∆CHE' cân tại C => C E ' H ^ = C H E ' ^
DBHF' cân tại B => B F ' H ^ = B H F ' ^
Mà => C H E ' ^ = B H F ' ^ (đối đỉnh)
=> C E ' H ^ = B F ' H ^
=> Tứ giác BCE'F' nội tiếp đường tròn tâm (O)
b, Có B F C ' ^ = B E ' C ^ = C H E ' ^ = C A B ^
Vậy A, F', E' cùng chắn BC dưới góc bằng nhau
=> 5 điểm B, F', A, E', C cùng thuộc một đường tròn tâm (O)
c, AF' = AE' (=AH) => AO là trung trực của EF => AO ^ E'F'. DHE'F' có EF là đường trung bình => EF//E'F'
=> AO ^ FE
d, A F H ^ = A E H ^ = 90 0 => AFHE nội tiếp đường tròn đường kính AH. Trong (O): Kẻ đường kính AD, lấy I trung điểm BC
=> OI = 1 2 AH, BC cố định => OI không đổi
=> Độ dài AH không đổi
=> Bán kính đường tròn ngoại tiếp ∆AEF không đổi

a) Ta có: \(\widehat{BFC}=90^0\)(CF\(\perp\)AB)
nên F nằm trên đường tròn đường kính BC(Định lí)(1)
Ta có: \(\widehat{BEC}=90^0\)(BE\(\perp\)AC)
nên E nằm trên đường tròn đường kính BC(Định lí)(2)
Từ (1) và (2) suy ra F,E cùng nằm trên đường tròn đường kính BC
hay B,F,E,C cùng thuộc một đường tròn(đpcm)

Đề bài yêu cầu gì vậy bạn?