Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

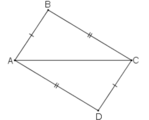
A B C D a)
ta có D là giao điểm của cung tròn tâm B với cung tròn tâm C=>BD là bán kính của cung tròn tâm B và CD là bán kính của cung tròn tâm C
ta có: DB là bán kính của cung tròn tâm B mà AC cũng là bán kính của cung tròn tâm B=> AC=BD
CM tương tự ta có: CD=AB
xét \(\Delta ABC\) và \(\Delta DCB\) có:
BD=AC(cmt)
AB=DC(cmt)
BC(chung)
\(\Rightarrow\Delta ABC=\Delta DCB\left(c.c.c\right)\)
=>\(\widehat{BAC}=\widehat{BDC}=80^o\)
b)
theo câu a, ta có:
\(\Delta ABC=\Delta DCB\Rightarrow\widehat{ABC}=\widehat{BCD}\)
=>CD//AB(2 góc slt)
A B C D Nếu bạn xem ko đc hình thì xem hình này cũng được, khi nãy mk vẽ quên căn
ở câu a, mk ko quen cách diễn đạt lớp 9 cho lắm nên thông cảm nhé

Xét ΔABC và ΔCDA, ta có:
AB = CD (theo cách vẽ)
AC cạnh chung
BC = AD (theo cách vẽ)
Suy ra: ΔABC = ΔCDA (c.c.c) ⇒ ∠(ACB) =∠(CAD) (hai góc tương ứng)
Vậy AD // BC ( vì có cặp góc so le trong bằng nhau)
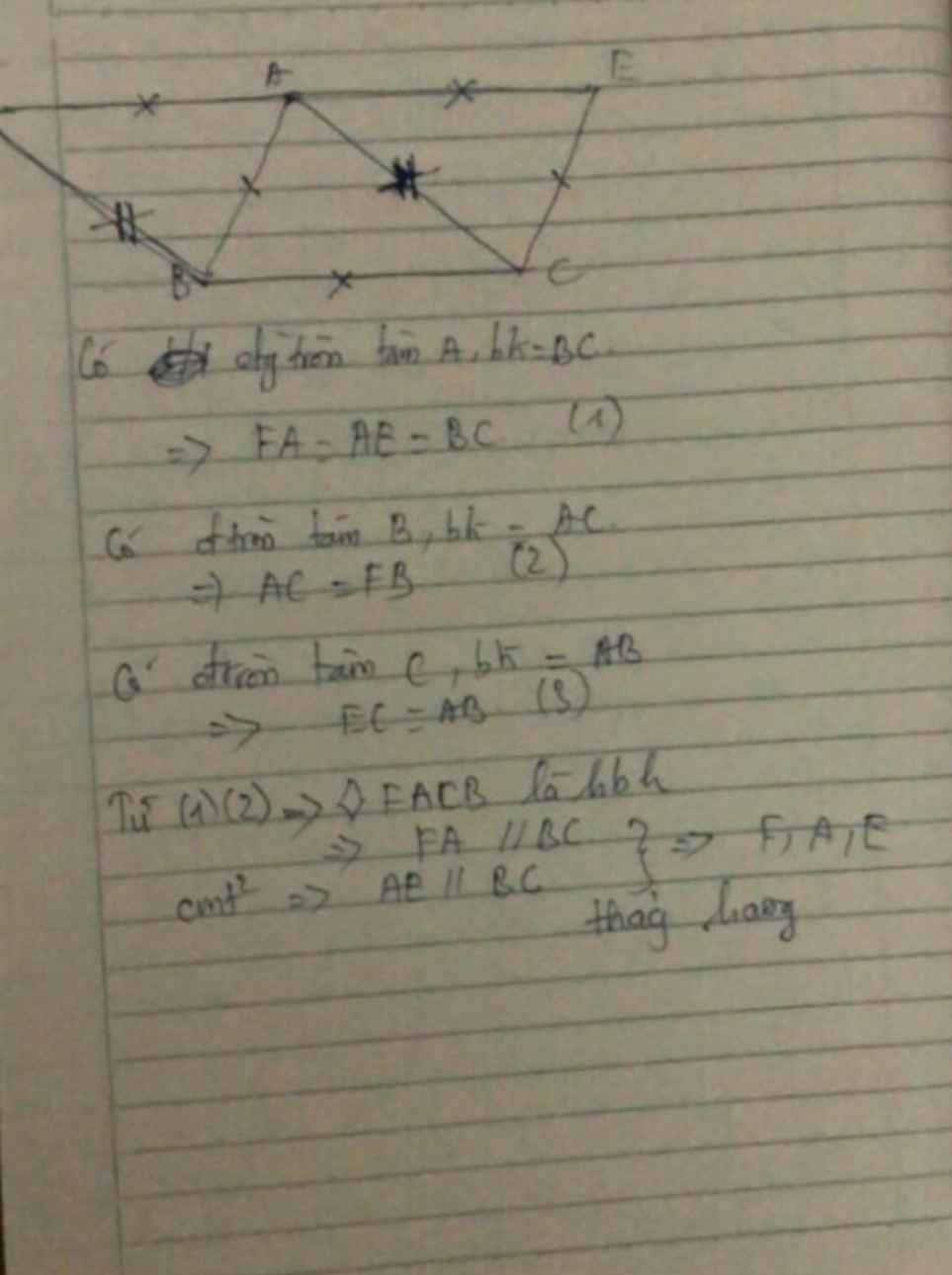
F là giao điểm của (A;BC) và (B;AC)
=>AF=BC và BF=AC
E là giao điểm của (A;BC) và (C;AB)
=>AE=BC và CE=AB
Xét ΔFAB và ΔCBA có
FA=CB
AB chung
FB=CA
Do đó: ΔFAB=ΔCBA
=>\(\hat{FAB}=\hat{CBA}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AF//BC
Xét ΔEAC và ΔBCA có
EA=BC
AC chung
EC=BA
Do đó: ΔEAC=ΔBCA
=>\(\hat{EAC}=\hat{BCA}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AE//BC
Ta có: AF//BC
AE//BC
mà AF,AE có điểm chung là A
nên F,A,E thẳng hàng
Để chứng minh ba điểm \(F , A , E\) thẳng hàng, ta sẽ sử dụng các tính chất hình học cơ bản của các đường tròn và tam giác.
Bước 1: Mô tả bài toán
Bước 2: Quan sát tính chất của các cung tròn
Bước 3: Sử dụng tính chất giao điểm của các đường tròn
Đường tròn tâm \(A\) bán kính \(B C\) cắt các cung tròn tâm \(C\) và \(B\) tại các điểm \(E\) và \(F\), điều này cho thấy rằng \(A , E , F\) là ba điểm đồng quy trên một đường tròn (điều này là một tính chất trong hình học Euclid, khi ba đường tròn giao nhau tại ba điểm).
Bước 4: Sử dụng tính chất của ba điểm đồng quy
Vì ba điểm \(A , E , F\) thuộc cùng một đường tròn, theo định lý về ba điểm đồng quy, chúng sẽ thẳng hàng.
Kết luận
Vậy, ba điểm \(F , A , E\) thẳng hàng.