K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 5 2019
\(\left(\frac{x}{2}+4.x^{-1}\right)^{18}\)
Số hạng tông quát trong khai triển:
\(C_{18}^k.\left(\frac{x}{2}\right)^k.\left(4x^{-1}\right)^{18-k}=C_{18}^k.\left(\frac{1}{2}\right)^k.4^{18-k}.x^{2k-18}\)
Số hạng ko chứa \(x\Rightarrow2k-18=0\Rightarrow k=9\)
Hệ số: \(C_{18}^9.\left(\frac{1}{2}\right)^9.4^9=2^9.C_{18}^9\)
25 tháng 3 2016
Gọi \(x_1,x_2\) là các nghiệm phương trình và \(r=\left|x_2\right|=\left|x_2\right|\) Khi đó :
\(\frac{p^2}{q^2}=\frac{\left(x_1+x_2\right)^2}{x_1x_2}=\frac{x_1}{x_2}+\frac{x_2}{x_1}+2=\frac{x_1\overline{x_2}}{r^2}+\frac{x_2\overline{x_1}}{r^2}+2=2+\frac{2}{r^2}Re\left(x_1\overline{x_2}\right)\)
Là số thực, hơn nữa :
\(Re\left(x_1\overline{x_2}\right)\ge-\left|x_1\overline{x_2}\right|=-r^2\)
Do đó \(\frac{p^2}{q^2}\ge0\)
vậy \(\frac{p}{q}\) là một số thực
Q
31 tháng 3 2017
- Xét a = 0 hàm số trở thành y = -9x + b. Trường hợp này hàm số không có cực trị.
- Xét a # 0. Ta có : y’ = 5a2x2 + 4ax – 9 ; y’= 0 ⇔ hoặc
- Với a < 0 ta có bảng biến thiên :
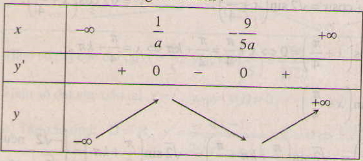
Theo giả thiết là điểm cực đại nên
. Theo yêu cầu bài toán thì
- Với a > 0 ta có bảng biến thiên :
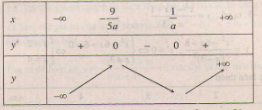
Vì là điểm cực đại nên
. Theo yêu cầu bài toán thì:
Vậy các giá trị a, b cần tìm là: hoặc
.
LT
26 tháng 4 2016
Ta có \(y'=3\left(x^2-m\right)\Rightarrow y'=0\Leftrightarrow x^2=m\)
Hàm số có 2 cực trị khi và chỉ khi \(m>0\). Khi đó tọa độ 2 điểm A, B là :
\(A\left(\sqrt{m}'-2m\sqrt{m}\right);B\left(-\sqrt{m};2m\sqrt{m}+2\right)\)
Suy ra \(\overrightarrow{AB}=\left(-2\sqrt{m};4m\sqrt{m}\right)\Rightarrow\overrightarrow{n}\left(2m;1\right)\) là vecto pháp tuyến của AB
Phương trình AB : 2mx + y -2 = 0
Suy ra \(d\left(I,AB\right)=\frac{\left|2m-1\right|}{\sqrt{1-4m^2}},AB=2\sqrt{m}.\sqrt{1+4m^2}\)
Do đó \(S_{\Delta IAB}=\frac{1}{2}.AB.d\left(I,AB\right)=\sqrt{m}\left|2m-1\right|\)
Mà \(S_{\Delta IAB}=\sqrt{18}\Rightarrow\sqrt{m}\left|2m-1\right|=\sqrt{18}\Rightarrow4m^3-4m^2+m-18=0\Leftrightarrow m=2\)
Vậy m = 2 là giá trị cần tìm
Khi nói đến phép cộng, chúng ta thường gặp các số đứng trước dấu bằng. Những con số này đóng vai trò quan trọng và chúng ta gọi chúng là "số hạng". Một phép cộng có thể bao gồm ít nhất hai số hạng hoặc nhiều hơn.
số số hạng nói dễ hiểu là cách tính xem có bao nhiêu số trong 1 dãy số
công thức tính số số hạng
số lớn nhất - số nhỏ nhất chia cho khoảng cách giữa các số và cộng thêm 1