Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

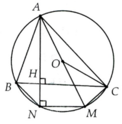
a, Ta có A C M ^ = 90 0 (góc nội tiếp)
b, Ta có ∆ABH:∆AMC(g.g)
=> B A H ^ = O A C ^ ; O C A ^ = O A C ^
=> B A H ^ = O C A ^
c, A N M ^ = 90 0
=> MNBC là hình thang
=> BC//MN => sđ B N ⏜ = sđ C M ⏜
=> C B N ^ = B C M ^ nên BCMN là hình thang cân

a: Xét (O) có
ΔACM nội tiếp
AM là đường kính
Do đó: ΔACM vuông tại C
hay \(\widehat{ACM}=90^0\)
b: \(\widehat{OAC}+\widehat{AMC}=90^0\)
\(\widehat{BAH}+\widehat{ABC}=90^0\)
mà \(\widehat{AMC}=\widehat{ABC}\)
nên \(\widehat{OAC}=\widehat{BAH}=\widehat{OCA}\)
Xét \(\Delta OAC\) có : \(OA=OC\left(=R\right)\left(gt\right)\)
\(\Rightarrow\Delta OAC\) cân tại O
\(\Rightarrow\widehat{OAC}=\widehat{ACO\left(2\right)}\)
Từ (1) và (2) \(\Rightarrow\widehat{BAH=\widehat{OCA}}\)
c) Xét \(\left(O\right)\), có : \(\widehat{ANM=90^0}\)
\(\Rightarrow MN\pm AN\)
\(MàBC\pm AN\left(gt\right)\)
\(\Rightarrow MN=BC\)
Xét tam giác \(BNMC\)\(cóMN=BC\left(cmt\right)\)
Tam giác BNMC là hình thang
Mà bốn đỉnh B,M,N,C
Vậy BMNC là tam giác cân

a: Xét (O) có
ΔACM nội tiếp
AM là đường kính
Do đó: ΔACM vuông tại C
b: \(\widehat{BAH}+\widehat{ABC}=90^0\)
\(\widehat{OAC}+\widehat{AMC}=90^0\)
mà \(\widehat{ABC}=\widehat{AMC}\left(=\dfrac{sđ\stackrel\frown{AC}}{2}\right)\)
nên \(\widehat{BAH}=\widehat{OAC}=\widehat{OCA}\)

c/ Gọi K là giao điểm của AC và HM
Vì ACHM là hình bình hành nên HK = HM
Mà OB = OM
\(\Rightarrow\)OK là đường trung bình của \(\Delta BHM\)
\(\Rightarrow OK=\frac{BH}{2}\left(1\right)\)
Ta lại có: \(\widehat{AOC}=2\widehat{ABC}=2.60^o=120^o\) (vì cùng chắn cung AC)
Mà \(OK⊥AC\)(Vì OK // BH và \(BH⊥AC\))
\(\Rightarrow\widehat{AOK}=\frac{\widehat{AOC}}{2}=\frac{120^o}{2}=60^o\)
\(\Rightarrow\Delta AOK\) là nửa tam giác đều
\(\Rightarrow OK=\frac{AO}{2}=\frac{R}{2}\left(2\right)\)
Từ (1) và (2) \(\Rightarrow BH=R=BO\)

Đây là nơi mà mỗi ý tưởng, mỗi trải nghiệm và mỗi bài học đều có giá trị. Chúng ta cùng nhau tạo nên một môi trường hỗ trợ lẫn nhau, phát triển tư duy, nâng cao kỹ năng và hoàn thiện bản thân. Hãy cùng nhau lan toả những nội dung tích cực, truyền cảm hứng và tránh những chia sẻ không mang lại giá trị thiết thực. Bằng sự tôn trọng, chân thành và tinh thần cầu tiến, chúng ta sẽ cùng nhau xây dựng một cộng đồng học tập lành mạnh, công bằng và truyền cảm hứng.
Xét (O) có
ΔACM nội tiếp
AM là đường kính
Do đó: ΔACM vuông tại C
=>\(\hat{ACM}=90^0\)
b: Xét (O) có
\(\hat{ABC};\hat{AMC}\) là các góc nội tiếp chắn cung AC
=>\(\hat{ABC}=\hat{AMC}\)
Ta có: \(\hat{ABC}+\hat{BAH}=90^0\) (ΔAHB vuông tại H)
\(\hat{AMC}+\hat{OAC}=90^0\) (ΔACM vuông tại C)
mà \(\hat{ABC}=\hat{AMC}\)
nên \(\hat{BAH}=\hat{OAC}\)
mà \(\hat{OAC}=\hat{OCA}\) (ΔOAC cân tại O)
nên \(\hat{BAH}=\hat{OCA}\)