Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1: ΔOED cân tại O
mà OH là trung tuyến
nên OH vuông góc DE
góc OHA=góc OBA=90 độ
=>O,H,B,A cùng thuộc 1 đường tròn
2: Xét ΔABD và ΔAEB có
góc ABD=góc AEB
góc BAD chung
=>ΔABD đồng dạng với ΔAEB
=>AB/AE=BD/EB
=>AB*EB=AE*BD

Bài này căng đấy =))
C E B A D O I H
a) Do AB là tiếp tuyến của (O) với B là tiếp điểm (gt)
nên : \(AB\perp OB\)( tc tiếp tuyến )
\(\Rightarrow\widehat{ABO}=90^o\)(1)
Do H là trung điểm của dây DE (gt)
nên : \(OH\perp DE\)( liên hệ giữa đường kính và dây )
\(\Rightarrow\widehat{AHO}=90^o\)(2)
- Xét tứ giác ABOH ta có :
+) \(\widehat{ABO}\)và \(\widehat{AHO}\)là hai góc đối diện
+) \(\widehat{ABO}+\widehat{AHO}=90^o+90^o=190^o\)( do (1) và (2))
=> ABOH là tứ giác nội tiếp
=> 4 điểm A , B , O , H thuộc cùng 1 đường tròn ( đpcm )
b) Ta có : +) \(\widehat{B_1}\)là góc giữa tia tiếp tuyến và dây cung chắn cung \(\widehat{BD}\)của (O)
+) \(\widehat{E_1}\)là góc nội tiếp chắn cung \(\widehat{BD}\)của (O)
\(\Rightarrow\widehat{B_1}=\widehat{E_1}=\frac{1}{2}sđ\widebat{BD}\)( tính chất )
Xét 2 tam giác : ABD và AEB có :
\(\widehat{B_1}=\widehat{E_1}\left(cmt\right)\)
\(\widehat{A}\)chung
\(\Rightarrow\Delta ABD~\Delta AEB\left(g.g\right)\)
\(\Rightarrow\frac{AB}{AE}=\frac{BD}{EB}\)( tỉ số đồng dạng )
\(\Rightarrow\frac{AB}{AE}=\frac{BD}{BE}\left(đpcm\right)\)
P/s : câu a) có nhiều cách chứng minh khác nữa bạn nhé . Bạn làm cách này có thể hay hơn là vì những gì đã nói ở trên về phương pháp trình bày và đồng thời chứng minh cũng áp dụng được cho nhiều bài khác ( Khi \(\widehat{ABO}\)và \(\widehat{AHO}\)không phải là những góc 90 độ )


a) Ta có \(IM//AE\)suy ra \(\widehat{MIH}=\widehat{EAH}\). Mà \(\widehat{EAH}=\widehat{ECH}\)nên \(\widehat{MIH}=\widehat{MCH}\). Suy ra tứ giác CIMH nội tiếp.
Dễ dàng chỉ ra được ED là tiếp tuyến của \(\left(O\right)\)suy ra \(\widehat{HED}=\widehat{HCE}\)\(\left(1\right)\)
Do tứ giác CIMH nội tiếp nên \(\widehat{CHM}=90^0\)suy ra \(\widehat{HCM}+\widehat{HMC}=90^0\)
Mà \(\widehat{HMD}+\widehat{HMC}=90^0\)nên \(\widehat{HCM}=\widehat{HMD}\)\(\left(2\right)\)
Từ \(\left(1\right)\)và \(\left(2\right)\)suy ra \(\widehat{HED}=\widehat{HMD}\)nên tứ giác EMHD nội tiếp. Do đó \(\widehat{HDM}=\widehat{HEM}\)mà \(\widehat{HEM}=\widehat{HCD}\)nên \(\widehat{HDM}=\widehat{HCD}\)
Từ đó chứng minh được BD là tiếp tuyến của \(\left(O_1\right)\)
b) Sử dụng tính chất đường nối tâm vuông góc với dây chung ta có: \(OO_2\perp HE,O_2O_1\perp HD\)và do \(EH\perp HD\)suy ra \(OO_2\perp O_2O_1\)
Dễ thấy \(\widehat{COM}=45^0\)suy ra \(\widehat{CAE}=45^0\)nên \(\widehat{O_2OO_1}=45^0\). \(\Delta O_2OO_1\)vuông cân tại \(O_2\)
Tứ giác OCDE là hình vuông cạnh R và \(O_2\) là trung điểm của DE nên ta tính được \(O_2O^2=\frac{5R^2}{4}\)
.Vậy diện tích \(\Delta O_2OO_1\) là\(\frac{5R^2}{8}\)

Chọn đáp án D
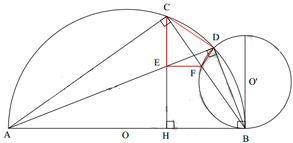

* Gọi (O’) là đường tròn đi qua D và tiếp xúc với AB tại B.
Đường tròn (O’) cắt CB tại F khác B. Chứng minh E F / / A B .
Ta có:

Hai góc ở vị trí đồng vị ⇒ E F / / A B

đừng spam bn ơi
giải hộ mình đi r mình k spam nữa