K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
KV
13 tháng 8
a) Số tiền Linh dùng mua bút bi:
50000 - 20000 = 30000 (đồng)
Giá tiền mỗi bút chì sau khi giảm:
x - 1000 (đồng)
Phân thức biểu thị số bút chì Linh mua được:
Phân thức biểu thị số bút bi Linh mua được:
b) Với x = 3000, số bút bi Linh mua được:
30000 : 3000 = 10 (bút)
23 tháng 8
a: ta có: EI⊥BF
AC⊥BF
Do đó: EI//AC
=>\(\hat{IEB}=\hat{ACB}\) (hai góc đồng vị)
mà \(\hat{ABC}=\hat{ACB}\) (ΔABC cân tại A)
nên \(\hat{KBE}=\hat{IEB}\)
Xét ΔKBE vuông tại K và ΔIEB vuông tại I có
BE chung
\(\hat{KBE}=\hat{IEB}\)
Do đó: ΔKBE=ΔIEB
=>EK=BI
b: Điểm D ở đâu vậy bạn?
11 tháng 8
1: \(\frac{1-a\cdot\sqrt{a}}{1-\sqrt{a}}=\frac{\left(1-\sqrt{a}\right)\left(1+\sqrt{a}+a\right)^{}}{1-\sqrt{a}}=1+\sqrt{a}+a\)
2: \(\frac{\sqrt{x+3}+\sqrt{x-3}}{\sqrt{x+3}-\sqrt{x-3}}=\frac{\left(\sqrt{x+3}+\sqrt{x-3}\right)\left(\sqrt{x+3}+\sqrt{x-3}\right)}{\left(\sqrt{x+3}-\sqrt{x-3}\right)\left(\sqrt{x+3}+\sqrt{x-3}\right)}\)
\(=\frac{\left(\sqrt{x+3}+\sqrt{x-3}\right)^2}{x+3-\left(x-3\right)}=\frac{x+3+x-3+2\sqrt{\left(x+3\right)\left(x-3\right)}}{6}\)
\(=\frac{2x+2\sqrt{x^2-9}}{6}=\frac{x+\sqrt{x^2-9}}{3}\)
4: \(\frac{3}{2\sqrt{9x}}=\frac{3}{2\cdot3\sqrt{x}}=\frac{1}{2\sqrt{x}}=\frac{\sqrt{x}}{2}\)
5: \(\frac{1}{2\sqrt{x}}=\frac{1\cdot\sqrt{x}}{2\sqrt{x}\cdot\sqrt{x}}=\frac{\sqrt{x}}{2x}\)
7: \(\frac{\sqrt{a^3}+a}{\sqrt{a}-1}=\frac{a\cdot\sqrt{a}+a}{\sqrt{a}-1}=\frac{a\left(\sqrt{a}+1\right)}{\sqrt{a}-1}=\frac{a\left(\sqrt{a}+1\right)\left(\sqrt{a}+1\right)}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}\)
\(=\frac{a\left(a+2\sqrt{a}+1\right)}{a-1}=\frac{a^2+2a\cdot\sqrt{a}+a}{a-1}\)
8: \(\frac{2}{\sqrt{a}+\sqrt{2b}}=\frac{2\cdot\left(\sqrt{a}-\sqrt{2b}\right)}{\left(\sqrt{a}+\sqrt{2b}\right)\left(\sqrt{a}-\sqrt{2b}\right)}=\frac{2\sqrt{a}-2\sqrt{2b}}{a-2b}\)
10: \(\frac{25}{\sqrt{a}-\sqrt{b}}=\frac{25\left(\sqrt{a}+\sqrt{b}\right)}{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}=\frac{25\sqrt{a}+25\sqrt{b}}{a-b}\)
11: \(-\frac{ab}{\sqrt{a}-\sqrt{b}}=-\frac{ab\left(\sqrt{a}+\sqrt{b}\right)}{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}=\frac{-ab\cdot\sqrt{a}-ab\cdot\sqrt{b}}{a-b}\)
LG
9
23 tháng 8
a; ABCD là hình thang cân
=>\(\hat{A}=\hat{B};\hat{C}=\hat{D}\)
\(\hat{A}+\hat{B}=\frac12\left(\hat{C}+\hat{D}\right)\)
=>\(2\cdot\hat{B}=\frac12\left(\hat{C}+\hat{C}\right)=\frac12\cdot2\cdot\hat{C}=\hat{C}\)
Ta có: AB//CD
=>\(\hat{B}+\hat{C}=180^0\)
=>\(\hat{B}+2\cdot\hat{B}=180^0\)
=>\(3\cdot\hat{B}=180^0\)
=>\(\hat{B}=60^0\)
\(\hat{C}=2\cdot\hat{B}=2\cdot60^0=120^0\)
\(\hat{D}=\hat{C}=120^0\)
\(\hat{A}=\hat{B}=60^0\)
b: ΔCAB vuông tại C
=>\(\hat{CAB}+\hat{CBA}=90^0\)
=>\(\hat{CAB}=90^0-60^0=30^0\)
Ta có: tia AC nằm giữa hai tia AD và AB
=>\(\hat{DAC}+\hat{BAC}=\hat{DAB}\)
=>\(\hat{DAC}=60^0-30^0=30^0\)
ta có: \(\hat{DAC}=\hat{BAC}\left(=30^0\right)\)
=>AC là phân giác của góc BAD
c: ta có: DC//AB
=>\(\hat{DCA}=\hat{CAB}\) (hai góc so le trong)
=>\(\hat{DCA}=30^0=\hat{DAC}\)
=>ΔDAC cân tại D
=>DC=DA
=>AD=a
Ta có: ABCD là hình thang cân
=>AD=BC
=>BC=a
Xét ΔCAB vuông tại C có \(\sin BAC=\frac{BC}{AB}\)
=>\(\frac{a}{AB}=\sin30=\frac12\)
=>AB=2a
ΔCAB vuông tại C
=>\(CA^2+CB^2=AB^2\)
=>\(CA^2=\left(2a\right)^2-a^2=3a^2\)
=>\(CA=a\sqrt3\)
Diện tích tam giác DAC là:
\(S_{DAC}=\frac12\cdot DA\cdot DC\cdot\sin ADC=\frac12\cdot a\cdot a\cdot\sin120=\frac{a^2\sqrt3}{4}\)
Diện tích tam giác ACB là:
\(S_{ACB}=\frac12\cdot CA\cdot CB=\frac12\cdot a\sqrt3\cdot a=\frac{a^2\sqrt3}{2}\)
Diện tích tam giác ABCD là:
\(S_{ABCD}=S_{DAC}+S_{CAB}=\frac{a^2\sqrt3}{4}+\frac{a^2\sqrt3}{2}=\frac{3a^2\sqrt3}{4}\)
S
subjects
CTVHS
20 tháng 8
thực hiện phép tính chia
\(a.\left(8x^4y^2-2x^3y^2+3x^2y^3\right):\left(2xy^2\right)\) (điều kiện: \(x;y\ne0)\)
\(=4x^3-x^2+\frac32xy\)
\(b.\left(-6x^3+5x^2y+4xy^2\right):\left(\frac14x\right)\) (điều kiện: \(x\ne0)\)
\(=-24x^2+20xy+16y^2\)
\(c.\left\lbrack7\cdot\left(y-x\right)^5+6\left(y-x\right)^4-2\left(x-y\right)^3+\left(y-x\right)^2\right\rbrack:\left(x-y\right)^2\) (điều kiện: \(x\ne y)\)
\(=7\left(y-x\right)^3+6\left(y-x\right)^2+2\left(y-x\right)+1\)
\(d.M\cdot\frac13xy^2=5x^4y^3-3x^3y^2+12x^2y\)
\(\Rightarrow M=\left(5x^4y^3-3x^3y^2+12x^2y\right):\left(\frac13xy^2\right)\)
\(M=15x^3y-9x^2+\frac{36x}{y}\)
\(e.\left(-6x^5y^3\right):M=2x^2y\)
\(\Rightarrow M=\left(-6x^5y^3\right):\left(2x^2y\right)\)
\(M=-3x^3y^2\)
\(\left(21x^7y^6-15x^6y^4+9x^4y^3\right):M\) (*)
thay M vào (*) ta được:
\(\left(21x^7y^6-15x^6y^4+9x^4y^3\right):\left(-3x^3y^2\right)\)
\(=-7x^4y^4+5x^3y^2-3xy\)
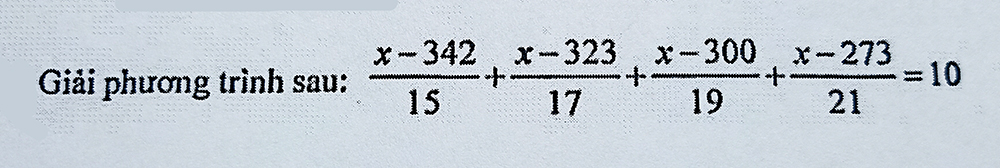
x
−
342
15
+
x
−
323
17
+
x
−
300
19
+
x
−
273
21
=
10
⇔
x
−
342
15
−
1
+
x
−
323
17
−
2
+
x
−
300
19
−
3
+
x
−
273
21
−
4
=
0
⇔
x
−
357
15
+
x
−
357
17
+
x
−
357
19
+
x
−
357
21
=
0
⇔
(
x
−
357
)
(
1
15
+
1
17
+
1
19
+
1
21
)
=
0
Vì
1
15
+
1
17
+
1
19
+
1
21
khác 0 nên x – 357 = 0 hay x = 357.
Vậy x = 357.
\(\dfrac{x-342}{15}+\dfrac{x-323}{17}+\dfrac{x-300}{19}+\dfrac{x-273}{21}=10\)
=>\(\left(\dfrac{x-342}{15}-1\right)+\left(\dfrac{x-323}{17}-2\right)+\left(\dfrac{x-300}{19}-3\right)+\left(\dfrac{x-273}{21}-4\right)=0\)
=>\(\left(x-357\right)\left(\dfrac{1}{15}+\dfrac{1}{17}+\dfrac{1}{19}+\dfrac{1}{21}\right)=0\)
=>x-357=0
=>x=357