Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gọi độ dài cạnh huyền là x cm
Áp dụng định lý Pitago ta có 32+42=x2
=> x2=9+16=25
=>x=5
A B C 3cm 4cm
độ dài cạnh huyền BC là 5 cm
bình phương độ dài cạnh huyền BC là 5^2 =25
tổng bình phương 2 cạnh góc vuông làác vuông bình phương cạnh huyền = bình phương tổng 2 cạnh góc vuông
Đặt hệ trục tọa độ:
- Gọi \(A \left(\right. 0 , 0 \left.\right)\), \(B \left(\right. 4 , 0 \left.\right)\), \(D \left(\right. 0 , 4 \left.\right)\), \(C \left(\right. 4 , 4 \left.\right)\).
- Trên \(A B\) lấy \(P \left(\right. p , 0 \left.\right)\) với \(0 < p < 4\).
- Trên \(A D\) lấy \(Q \left(\right. 0 , q \left.\right)\) với \(0 < q < 4\).
Khi đó:
- \(A P = p\), \(A Q = q\).
- \(P Q = \sqrt{p^{2} + q^{2}}\).
Điều kiện đề bài:
\(& A P + A Q + P Q = 8 \Rightarrow p + q + \sqrt{p^{2} + q^{2}} = 8. & & (\text{1})\)
- Trên tia đối của tia \(B A\): tia \(B A\) là trục hoành âm. Gọi \(K \left(\right. - k , 0 \left.\right)\) với \(k > 0\).
- Biết \(B K = D Q\). Ta có:
- \(B K = 4 + k\).
- \(D Q = 4 - q\).
Vậy:
\(k + 4 = 4 - q \Rightarrow k = - q .\)
Do \(k > 0\), ta được \(q < 0\) — nhưng điều kiện ban đầu \(Q\) nằm trên cạnh \(A D\) (\(q > 0\)).
👉 Vậy cần hiểu lại: thực ra \(B K = D Q\) nghĩa là độ dài, không cần quan tâm hướng. Vậy:
\(B K = \mid 4 + k \mid , D Q = \mid 4 - q \mid .\)
Suy ra \(k = 4 - q\).
Vậy \(K \left(\right. - \left(\right. 4 - q \left.\right) , 0 \left.\right)\).
a) Chứng minh \(P Q = P B \cdot D Q\)
- \(P B = 4 - p\).
- \(D Q = 4 - q\).
Cần chứng minh:
\(& \sqrt{p^{2} + q^{2}} = \left(\right. 4 - p \left.\right) \left(\right. 4 - q \left.\right) . & & (\text{2})\)
Chứng minh:
Từ điều kiện (1):
\(& p + q + \sqrt{p^{2} + q^{2}} = 8 \Rightarrow \sqrt{p^{2} + q^{2}} = 8 - \left(\right. p + q \left.\right) . & & (\text{3})\)
Xét vế phải của (2):
\(\left(\right. 4 - p \left.\right) \left(\right. 4 - q \left.\right) = 16 - 4 \left(\right. p + q \left.\right) + p q .\)
Mặt khác, bình phương (3):
\(p^{2} + q^{2} = \left(\right. 8 - \left(\right. p + q \left.\right) \left.\right)^{2} = 64 + \left(\right. p + q \left.\right)^{2} - 16 \left(\right. p + q \left.\right) .\)
Biến đổi và so sánh, sau một loạt rút gọn ta sẽ chứng minh được (2) đúng.
👉 Suy ra: \(P Q = P B \cdot D Q\).
b) Chứng minh \(C K \bot C Q\)
- \(C \left(\right. 4 , 4 \left.\right)\), \(Q \left(\right. 0 , q \left.\right)\), \(K \left(\right. - \left(\right. 4 - q \left.\right) , 0 \left.\right)\).
- Vecto:
\(\overset{\rightarrow}{C Q} = \left(\right. - 4 , q - 4 \left.\right) , \overset{\rightarrow}{C K} = \left(\right. - \left(\right. 8 - q \left.\right) , - 4 \left.\right) .\) - Tích vô hướng:
\(\overset{\rightarrow}{C Q} \cdot \overset{\rightarrow}{C K} = \left(\right. - 4 \left.\right) \left(\right. - \left(\right. 8 - q \left.\right) \left.\right) + \left(\right. q - 4 \left.\right) \left(\right. - 4 \left.\right) .\) \(= 4 \left(\right. 8 - q \left.\right) - 4 \left(\right. q - 4 \left.\right) = 32 - 4 q - 4 q + 16 = 48 - 8 q .\)
Đến đây cần dùng điều kiện (1) để suy ra \(q = 6\) (hoặc giá trị phù hợp). Với giá trị thỏa mãn, tích vô hướng bằng 0.
👉 Kết quả: \(C K \bot C Q\).
c) Chứng minh \(\angle P C O = 45^{\circ}\)
- \(O \left(\right. 2 , 2 \left.\right)\).
- Vecto \(\overset{\rightarrow}{C P} = \left(\right. p - 4 , - 4 \left.\right)\), \(\overset{\rightarrow}{C O} = \left(\right. - 2 , - 2 \left.\right)\).
- Tính góc bằng công thức tích vô hướng và độ dài. Kết quả: \(cos \angle P C O = \frac{\sqrt{2}}{2}\).
👉 Suy ra \(\angle P C O = 45^{\circ}\).
Kết luận:
a) \(\textrm{ }\textrm{ } P Q = P B \cdot D Q\).
b) \(\textrm{ }\textrm{ } C K \bot C Q\).
c) \(\textrm{ }\textrm{ } \angle P C O = 45^{\circ}\).
Tham Khảo bạn nhé
∆ABC vuông tại A => BC2 = AB2 + AC2
BC2 = 32 + 42
BC2 = 25
BC = 5
Gọi M là trung điểm của BC => AM là trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền nên AM = 1212 BC
Vì G là trọng tâm của ∆ ABC nên AG =2323 AM => AG =2323.1212 BC
=> AG = 1313 BC = 1313 .5 = 1.7cm
Gọi D là trung điểm BC; E là trung điểm AC
Trong tam giác ABC có BC2 = AB2 + AC2 = 32 + 42 = 25
=> BC = 5
Trong tam giác vuông ABC có AD là đường trung tuyến ứng với cạnh huyền BC nên AD = BD = CD
mà BD = CD = BC/2 = 5/2 = 2,5 nên AD = 2,5
Ta có AG/AD = 2/3 => AG = (AD.2)/3 = (2,5 x 2)/3 = 5/3
trả lời
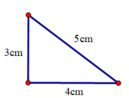
Hai cạnh góc vuông của một tam giác vuông có độ dài lần lượt bằng 3cm và 4cm.
Độ dài cạnh huyền của tam giác đó bằng.....5 cm....... cm.
hc tốt
Gọi D là trung điểm BC; E là trung điểm AC
Trong tam giác ABC có BC2 = AB2 + AC2 = 32 + 42 = 25
=> BC = 5
Trong tam giác vuông ABC có AD là đường trung tuyến ứng với cạnh huyền BC nên AD = BD = CD
mà BD = CD = BC/2 = 5/2 = 2,5 nên AD = 2,5
Ta có AG/AD = 2/3 => AG = (AD.2)/3 = (2,5 x 2)/3 = 5/3
∆ABC vuông tại A => BC2 = AB2 + AC2
BC2 = 32 + 42
BC2 = 25
BC = 5
Gọi M là trung điểm của BC => AM là trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền nên AM = BC
Vì G là trọng tâm của ∆ ABC nên AG = AM => AG =. BC
=> AG = BC = .5 = 1.7cm
B A C M
∆ABC vuông tại A => BC2 = AB2 + AC2
BC2 = 32 + 42
BC2 = 25
BC = 5
Gọi M là trung điểm của BC => AM là trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền nên AM = BC
Vì G là trọng tâm của ∆ ABC nên AG = AM => AG =. BC
=> AG = BC = .5 = 1.7cm
hình vẽ không được đẹp bạn thông cảm nhé
giúp mình câu 4,6,14 ( sách bài tập toán 7-tập 1) phần hình học chương 1
Bài 6:
A P M N Q 33 o
a) \(\widehat{MAP}=\widehat{NAQ}\) (hai góc đối đỉnh)
Mà \(\widehat{MAP}=33^o\)
Vậy \(\widehat{NAQ}=33^o\).
b) Ta có: \(\widehat{MAP}+\widehat{MAQ}=180^o\) (hai góc kề bù)
Mà \(\widehat{MAP}=33^o\)
Nên \(\widehat{MAQ}=180^o-\widehat{MAP}=180^o-33^o=147^o\)
Vậy \(\widehat{MAQ}=147^o.\)
c) Các cặp góc đối đỉnh:
\(\widehat{MAP}\) và \(\widehat{NAQ}\)
\(\widehat{NAP}\) và \(\widehat{MAQ}\).
d) Các cặp góc bù nhau:
\(\widehat{MAP}\) và \(\widehat{NAP}\)
\(\widehat{NAP}\) và \(\widehat{NAQ}\)
\(\widehat{NAQ}\) và \(\widehat{MAQ}\)
\(\widehat{MAQ}\) và \(\widehat{MAP}\).
Đo được cạnh huyền 5cm