BB
Vẽ hình và giải chi tiết giúp mình nhé. Mình đang cần gấp.
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
3
11 tháng 1 2023
a: Xét tứ giác DIHK có
góc DIH=góc DKH=góc KDI=90 độ
nên DIHK là hình chữ nhật
b: Xét tứ giác IHAK có
IH//AK
IH=AK
Do đó: IHAK là hình bình hành
=>B là trung điểm chung của IA và HK
Xét ΔIKA có IC/IK=IB/IA
nên BC//KA
Xét ΔIDA có IB/IA=IM/ID
nên BM//DA
=>B,C,M thẳng hàng
trong công cụ 
để kiểm tra trung điểm AC và BD có trùng nhau không.
QT
Quoc Tran Anh Le
Giáo viên
14 tháng 1 2024
a) Dùng 
trong công cụ 
để kiểm tra trung điểm AC và BD, ta thấy trung điểm AC và BD trùng nhau.
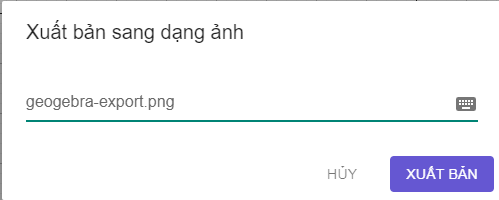
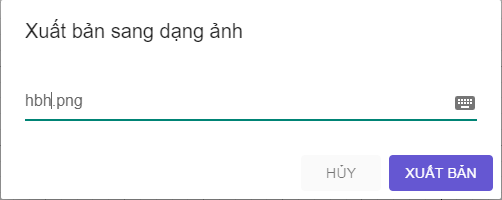
b) Lưu hình vẽ ở HĐ2 thành tệp hbh.png.
Vào Hồ sơ → Chọn Xuất bản → Chọn PNG image (.png).
Ta đổi tên tệp thành hbh (như hình vẽ), sau đó chọn xuất bản.
Bước 1. Vẽ đoạn thẳng AB và có độ dài 4 cm tương tự như Bước 1 của HĐ1.
Bước 2. Vẽ điểm C sao cho BC = 4 cm.
Chọn công cụ 
→ Chọn 
→ Nháy chuột vào điểm B, nhập bán kính bằng 4.
Chọn công cụ 
→ Chọn 
→ Chọn điểm C bất kỳ nằm trên đường tròn tâm B.
Chọn công cụ 
→ Chọn 
→ Nháy chuột vào điểm C, nhập bán kính bằng 4.
Chọn công cụ 
→ Chọn 
→ Lần lượt nháy chuột đường tròn tâm A và đường tròn C.
Chọn công cụ 
để nối B với C, C với D, D với A.
Bước 3. Ẩn đường tròn và thu được hình thoi ABCD.
MP
0
S
subjects
CTVHS
23 giờ trước (15:21)
10) đkxđ: \(x\ne\pm3\)
\(\frac{7}{a^2-9}+\frac{5}{a-3}+\frac{1}{a+3}=\frac{7}{\left(a-3\right)\left(a+3\right)}+\frac{5\cdot\left(a+3\right)}{\left(a+3\right)\left(a-3\right)}+\frac{a-3}{\left(a+3\right)\left(a-3\right)}\)
\(=\frac{7+5a+15+a-3}{\left(a+3\right)\left(a-3\right)}=\frac{6a+19}{\left(a+3\right)\left(a-3\right)}\)
11) đkxđ: \(x\ne-1\)
\(\frac{2x-1}{x^3+1}+\frac{2x}{x^2-x+1}-\frac{x}{x+1}+2\)
\(=\frac{2x-1}{\left(x+1\right)\left(x^2-x+1\right)}+\frac{2x\cdot\left(x+1\right)}{\left(x+1\right)\left(x^2-x+1\right)}-\frac{x\cdot\left(x^2-x+1\right)}{\left(x+1\right)\left(x^2-x+1\right)}+\frac{2\left(x+1\right)\left(x^2-x+1\right)}{\left(x+1\right)\left(x^2-x+1\right)}\)
\(\) \(=\frac{2x-1+2x^2+2x-x^3+x^2-x+2x^3+2}{\left(x+1\right)\left(x^2-x+1\right)}\)
\(=\frac{x^3+3x^2+3x+1}{\left(x+1\right)\left(x^2-x+1\right)}\)
\(=\frac{\left(x+1\right)^3}{\left(x+1\right)\left(x^2-x+1\right)}\)
\(=\frac{\left(x+1\right)^2}{x^2-x+1}\)
13) đkxđ: \(x\ne\pm\frac32\)
\(\frac{5}{2x-3}+\frac{2}{2x+3}-\frac{2x+5}{9-4x^2}\)
\(=\frac{5\cdot\left(2x+3\right)}{\left(2x-3\right)\left(2x+3\right)}+\frac{2\cdot\left(2x-3\right)}{\left(2x-3\right)\left(2x+3\right)}+\frac{2x+5}{\left(2x-3\right)\left(2x+3\right)}\)
\(=\frac{10x+15+4x-6+2x+5}{\left(2x-3\right)\left(2x+3\right)}\)
\(=\frac{16x+14}{\left(2x-3\right)\left(2x+3\right)}\)
QT
1
11 tháng 9 2023
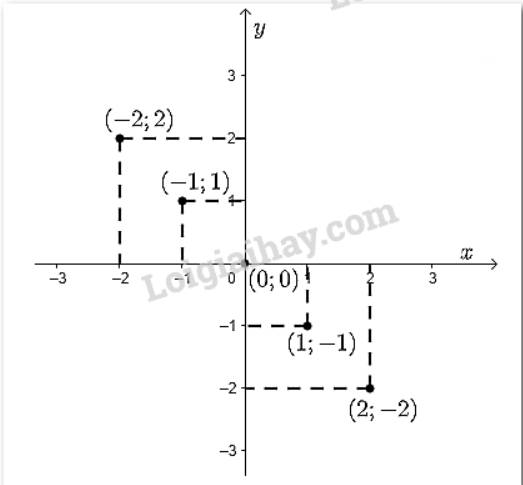
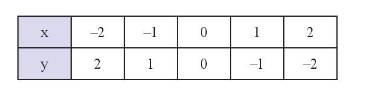
Đồ thị hàm số là tập hợp các điểm có tọa độ \(\left( { - 2;2} \right);\left( { - 1;1} \right);\left( {0;0} \right);\left( {1; - 1} \right);\left( {2; - 2} \right)\) được vẽ trên mặt phẳng tọa độ như hình dưới đây:
trong công cụ 
để kiểm tra DE có bằng 4 cm không.
QT
Quoc Tran Anh Le
Giáo viên
14 tháng 1 2024
a) Dùng 
trong công cụ 
để kiểm tra DE, ta thấy độ dài đoạn thẳng DE bằng 4 cm.
Vào Hồ sơ → Chọn Xuất bản → Chọn PNG image (.png).
Ta đổi tên tệp thành hbh (như hình vẽ), sau đó chọn xuất bản.
c) Vẽ hình thang cân ADEC có AD // EC, AD = 6 cm, CE = 4 cm, AC = DE = 3 cm theo các bước sau:
Bước 1. Vẽ đoạn thẳng AB và có độ dài bằng AD – EC = 2 cm tương tự như Bước 1 của HĐ1.
Bước 2. Vẽ tam giác ABC có BC = 3 cm (độ dài của DE), AC = 3 cm.
Chọn công cụ 
→ Chọn 
→ Nháy chuột vào điểm A, nhập bán kính bằng 3.
Chọn công cụ → Chọn → Nháy chuột vào điểm B, nhập bán kính bằng 3.
Chọn công cụ 
→ Chọn 
→ Lần lượt nháy chuột vào hai đường tròn vừa vẽ, ta được 2 giao điểm, chọn 1 điểm là điểm C.
Chọn công cụ 
→ Chọn 
→ Chọn điểm A → Chọn điểm C.
Chọn công cụ → Chọn → Chọn điểm B → Chọn điểm C.
Chọn công cụ → Chọn → Nháy chuột vào điểm A, nhập bán kính bằng 6.
Chọn công cụ → Chọn 
→ Nháy chuột lần lượt vào các điểm A, B.
Chọn công cụ → Chọn 
→ Lần lượt nháy chuột vào tia AB và đường tròn vừa vẽ, ta được điểm D.
Bước 4. Vẽ điểm E sao cho DE // BC và CE // AB.
Chọn công cụ 
→ Chọn 
→ Nháy chuột vào điểm C → Nháy chuột vào đoạn thẳng AB.
Chọn công cụ → Chọn → Nháy chuột vào điểm D → Nháy chuột vào đoạn thẳng CB.
Chọn công cụ 
→ Chọn 
→ Lần lượt nháy chuột vào đường thẳng vừa vẽ.
Ẩn các đường tròn, các đường thẳng, đoạn thẳng AB, BC và điểm B. Chọn công cụ để nối A với D, D với E, E với C và thu được hình thang cân ADEC thỏa mãn yêu cầu đề bài.
+Dùng +trong+công+cụ +để+kiểm+tra+trung+điểm+AC+và+BD+có+trùng+nhau+không.b)+Lưu+hình+vẽ+ở+HĐ2+thành+tệp+hbh.png.c)+Tương+tự,+hãy+vẽ+một+hình+thoi+ABCD+có+cạnh+4+cm.){kind=link}
+Dùng +trong+công+cụ +để+kiểm+tra+DE+có+bằng+4+cm+không.b)+Lưu+hình+vẽ+ở+HĐ3+thành+tệp+hth.png.c)+Tương+tự,+hãy+vẽ+hình+thang+cân+ADEC+có+AD+//+EC,+AD+=+6+cm,+CE+=+4+cm,+AC+=+DE+=+3+cm.){kind=link}
P
Phong
CTVHS
19 tháng 10 2023
a) Xét tứ giác ABCD ta có:
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\)
\(\Rightarrow\widehat{D}=360^o-102^o-102^o-102^o\)
\(\Rightarrow\widehat{D}=54^o\)
b) Xét tam giác vuông AOD ta có:
\(AD^2=OD^2+OA^2\)
\(\Rightarrow OA=\sqrt{AD^2-OD^2}\)
\(\Rightarrow OA=\sqrt{30^2-26,7^2}\approx13,7\left(cm\right)\)
Xét tam giác vuông AOB ta có:
\(AB^2=OA^2+OB^2\)
\(\Rightarrow OB=\sqrt{AB^2-OA^2}\)
\(\Rightarrow OB=\sqrt{17,5^2-13,7^2}\approx10,9\left(cm\right)\)
Độ dài đường chéo BD là:
\(BD=OB+OD=26,7+10,9\approx37,6\left(cm\right)\)
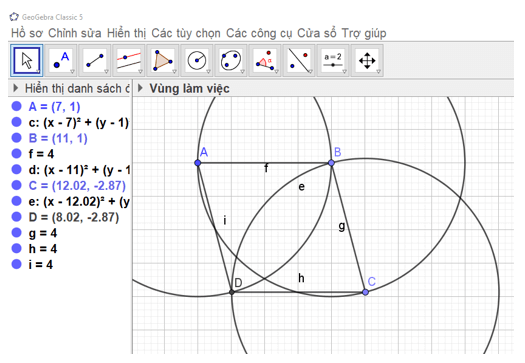
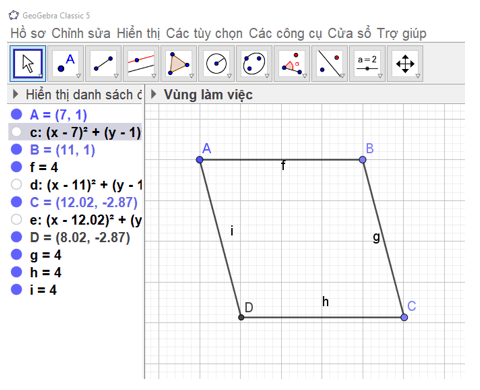
a: Xét tứ giác BHCD có
M là trung điểm chung của BC và HD
Do đó: BHCD là hình bình hành
b: BHCD là hình bình hành
=>BH//CDvà BD//CH
BH//CD
AC vuông góc BH
Do đó: CA vuông góc CD
=>ΔCAD vuông tại C
CH//BD
CH vuông góc AB
Do đó: BD vuông góc AB
=>ΔABD vuông tại B
c: \(\widehat{ABD}=\widehat{ACD}=90^0\)
=>ABDC là tứ giác nội tiếp đường tròn đường kính AD
=>ABDC nội tiếp (I)
=>IA=IB=ID=IC
Bạn ơi vẽ hình giúp với