Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b)
các góc băng nhau:
ONTˆONT^ == NPKˆNPK^ (đồng vị)
NTOˆNTO^ == PITˆPIT^ (đồng vị)
IPOˆIPO^ == PORˆPOR^ (sole trong)
RONˆRON^ == ONTˆONT^ (sole trong)
-các góc bù nhau:
NTIˆNTI^ và NTOˆNTO^
-các góc ngòai của tam giác TNO:
TNPˆTNP^ ; ITNˆITN^
-tổng các góc trong của tứ giác PROI: 360o
-tổng các góc trong của tứ giác PNTI: 360o

Bổ sung đề: I là trung điểm của PQ
=>MI vuông góc PQ tại I
IP=IQ=6/2=3cm
MI=căn 5^2-3^2=4cm

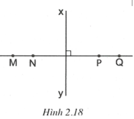
Ta có M N ⊥ x y ; P Q ⊥ x y (vì xy là đường trung trực của NP). Qua điểm N chỉ vẽ được một đường thẳng vuông góc với xy, suy ra ba điểm M, N, P thẳng hàng. (1)
Ta có N P ⊥ x y ; P Q ⊥ x y . Qua điểm P chỉ vẽ được một đường thẳng vuông góc với xy, suy ra ba điểm N, P, Q thẳng hàng. (2)
Từ (1) và (2) suy ra các điểm M, N, P, Q thẳng hàng vì chúng cùng thuộc đường thẳng NP

1:Xét ΔAMP và ΔAMQ có
AM chung
MP=MQ
AP=AQ
Do đó: ΔAMP=ΔAMQ
=>\(\hat{AMP}=\hat{AMQ}\)
mà \(\hat{AMP}+\hat{AMQ}=180^0\) (hai góc kề bù)
nên \(\hat{AMP}=\hat{AMQ}=\frac{180^0}{2}=90^0\)
=>AM⊥PQ
mà M là trung điểm của PQ
nên AM là đường trung trực của PQ
2: Xét ΔMAQ vuông tại M và ΔMBP vuông tại M có
MA=MB
MQ=MP
Do đó: ΔMAQ=ΔMBP
3:
a: ΔAMP=ΔAMQ
=>\(\hat{MAP}=\hat{MAQ}\)
Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
\(\hat{EAM}=\hat{FAM}\)
Do đó: ΔAEM=ΔAFM
=>\(\hat{AME}=\hat{AMF}\)
=>MA là phân giác của góc EMF
b: ΔAEM=ΔAFM
=>AE=AF
=>ΔAEF cân tại A
Xét ΔAPQ có \(\frac{AE}{AP}=\frac{AF}{AQ}\)
nên EF//PQ
KO CARE