Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
*Giải bài toán*
Gọi số hạng đầu là \(a_1\) và công sai là \(d\). Số hạng tổng quát là \(a_n = a_1 + (n-1)d\).
*Điều kiện 1*
Tổng số báo danh của 5 học sinh đứng giữa hàng là gấp 5 lần số báo danh của học sinh đứng thứ 8:
\[a_6 + a_7 + a_8 + a_9 + a_{10} = 5a_8\]
\[5a_1 + 35d = 5(a_1 + 7d)\]
Điều này luôn đúng.
*Điều kiện 2*
Tổng số báo danh của học sinh ở vị trí chẵn bằng 3 lần tổng số báo danh của học sinh ở vị trí lẻ:
\[S_{chẵn} = 3S_{lẻ}\]
Với \(n = 22\), ta có:
\[S_{chẵn} = a_2 + a_4 + ... + a_{22}\]
\[S_{lẻ} = a_1 + a_3 + ... + a_{21}\]
\[11a_1 + 110d = 3(11a_1 + 55d)\]
\[11a_1 + 110d = 33a_1 + 165d\]
\[22a_1 = -55d\]
\[2a_1 = -5d\]
*Điều kiện 3*
\[S_3 - S_4 = 2025\]
Với \(n = 22\), \(k = 7\), \(l = 5\):
\[S_3 = 7a_1 + 77d\]
\[S_4 = 5a_1 + 55d\]
\[2a_1 + 22d = 2025\]
*Điều kiện 4*
\[a_{22} - a_{11} = 11d\]
\[11d = 11d\]
\[n = 22\]
*Tìm \(a_1\) và \(d\)*
Từ \(2a_1 = -5d\) và \(2a_1 + 22d = 2025\):
\[2a_1 = -5d\]
\[-5d + 22d = 2025\]
\[17d = 2025\]
\[d = \frac{2025}{17} = 119\]
\[2a_1 = -5 \cdot 119\]
\[a_1 = -\frac{595}{2}\]
*Kết quả*
\[n = 22\]
\[a_1 = -\frac{595}{2}\]
\[d = 119\]
1. số tự nhiên có dạng abce ( nhớ gạch trê đầu ( vì đây là số tự nhiên))
* ta có h là :
h= mn
trong đó tập hợp mn là {0,1}
=> có 2 trường hợp xảy ra
(m,n)=(1,0) hoặc (0,1)
* ta có số tự nhiên abhe có tập hợp {h,2,3,4,5,6,7,8,9}
a có 9 cách chọn
b có 8 cách chọn
c có 7 cách chọn
e có 6 cách chọn
vậy có 9*8*7*6=3024 số
*ta phải loại trường hợp h đứng đầu và có dạng 01
trường hợp h đứng đầu và có dạng 01 có số cách chọn là :
a có 1 cách chọn là h
b có 8 cách
c có 7 cách
e có 6 cách
=> có 1*8*7*6=336 số
vậy số tự nhiên theo yêu cầu đề bài có tổng cộng
3024 - 332688 số
0 chắc
Ta đi tìm số cách chọn ra 5 bạn mà trong đó có cả hai bạn Thùy và Thiện.
Bước 1: Chọn nhóm 3 em trong 13 em, trừ Thùy và Thiện thì có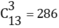
cách.
Bước 2: Ghép 2 em Thùy và Thiện có 1 cách.
Vậy theo quy tắc nhân thì có 286 cách chọn 5 em trong đó cả Thùy hoặc Thiện đều được chọn.
- Chọn 5 em bất kì trong số 15 em có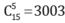
cách. Vậy theo yêu cầu đề bài thì có tất cả 3003-286=2717 cách chọn mà trong đó có ít nhất một trong hai em Thùy và Thiện không được chọn.
Chọn C.