Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án C
Lấy ngẫu nhiên 4 mẫu có: Ω = C 15 4
Gọi X là biến cố:”mẫu thịt của cả 3 quầy A,B,C đều được chọn”
TH1: 2 mẫu quầy A,1 mẫu quầy B và 1 mẫu quầy C có: C 4 2 . C 5 1 . C 6 1 cách.
TH2: 1 mẫu quầy A,2 mẫu quầy B và 1 mẫu quầy C có: C 4 1 . C 5 2 . C 5 1 cách
TH3: 1 mẫu quầy A, 1 mẫu quầy B và 2 mẫu quầy C có: C 4 1 . C 5 1 . C 6 2 cách
Vậy xác suất cần tìm là:
*Giải bài toán*
Gọi số hạng đầu là \(a_1\) và công sai là \(d\). Số hạng tổng quát là \(a_n = a_1 + (n-1)d\).
*Điều kiện 1*
Tổng số báo danh của 5 học sinh đứng giữa hàng là gấp 5 lần số báo danh của học sinh đứng thứ 8:
\[a_6 + a_7 + a_8 + a_9 + a_{10} = 5a_8\]
\[5a_1 + 35d = 5(a_1 + 7d)\]
Điều này luôn đúng.
*Điều kiện 2*
Tổng số báo danh của học sinh ở vị trí chẵn bằng 3 lần tổng số báo danh của học sinh ở vị trí lẻ:
\[S_{chẵn} = 3S_{lẻ}\]
Với \(n = 22\), ta có:
\[S_{chẵn} = a_2 + a_4 + ... + a_{22}\]
\[S_{lẻ} = a_1 + a_3 + ... + a_{21}\]
\[11a_1 + 110d = 3(11a_1 + 55d)\]
\[11a_1 + 110d = 33a_1 + 165d\]
\[22a_1 = -55d\]
\[2a_1 = -5d\]
*Điều kiện 3*
\[S_3 - S_4 = 2025\]
Với \(n = 22\), \(k = 7\), \(l = 5\):
\[S_3 = 7a_1 + 77d\]
\[S_4 = 5a_1 + 55d\]
\[2a_1 + 22d = 2025\]
*Điều kiện 4*
\[a_{22} - a_{11} = 11d\]
\[11d = 11d\]
\[n = 22\]
*Tìm \(a_1\) và \(d\)*
Từ \(2a_1 = -5d\) và \(2a_1 + 22d = 2025\):
\[2a_1 = -5d\]
\[-5d + 22d = 2025\]
\[17d = 2025\]
\[d = \frac{2025}{17} = 119\]
\[2a_1 = -5 \cdot 119\]
\[a_1 = -\frac{595}{2}\]
*Kết quả*
\[n = 22\]
\[a_1 = -\frac{595}{2}\]
\[d = 119\]
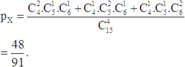
Tất cả các cạnh của tứ giác là đường chéo khi 4 đỉnh đó ko có 2 đỉnh nào liền kề nhau.
Cố định một đỉnh, có n cách chọn
Chọn đỉnh thứ 2 cách đỉnh thứ nhất \(x_1\) đỉnh, đỉnh thứ 3 cách đỉnh 2 \(x_2\) ; đỉnh thứ 4 cách đỉnh thứ 3 \(x_3\) và cách đỉnh thứ nhất \(x_4\) đỉnh (với \(x_i\ge1\))
\(\Rightarrow x_1+x_2+x_3+x_4=n-4\)
Theo nguyên lý chia kẹo Euler, số nghiệm của pt trên là: \(C_{n-5}^3\)
Vậy số đa giác thỏa mãn là: \(\frac{nC_{n-5}^3}{4}\)
Xác suất: \(P=\frac{nC_{n-5}^3}{4C_n^4}=\frac{30}{91}\) \(\Rightarrow n=15\)
Đáp án C
Lấy 4 mẫu thịt lợn trong 15 mẫu có C 5 4 = 1365 cách
Gọi A là biến cô “mẫu thịt của cả 3 mẫu A, B, C đều được chọn”
Khi đó Ω A = 720 cách