Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

I don't now
or no I don't
..................
sorry

a: Xét ΔOAC và ΔOBC có
OA=OB
\(\widehat{AOC}=\widehat{BOC}\)
OC chung
Do đó: ΔOAC=ΔOBC
=>AC=BC
=>C là trung điểm của AB
Ta có: CA=CB
=>C nằm trên đường trung trực của AB(1)
ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra OC là đường trung trực của AB
=>CO\(\perp\)AB
b: Xét ΔOAC và ΔMBC có
CO=CM
\(\widehat{OCA}=\widehat{MCB}=90^0\)
CA=CB
Do đó: ΔOAC=ΔMBC
=>\(\widehat{OAC}=\widehat{MBC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên OA//BM
Xét ΔCBO vuông tại C và ΔCAM vuông tại C có
CB=CA
CO=CM
Do đó: ΔCBO=ΔCAM
=>\(\widehat{CBO}=\widehat{CAM}\)
mà hai góc này là hai góc ở vị trí so le trong
nên BO//AM
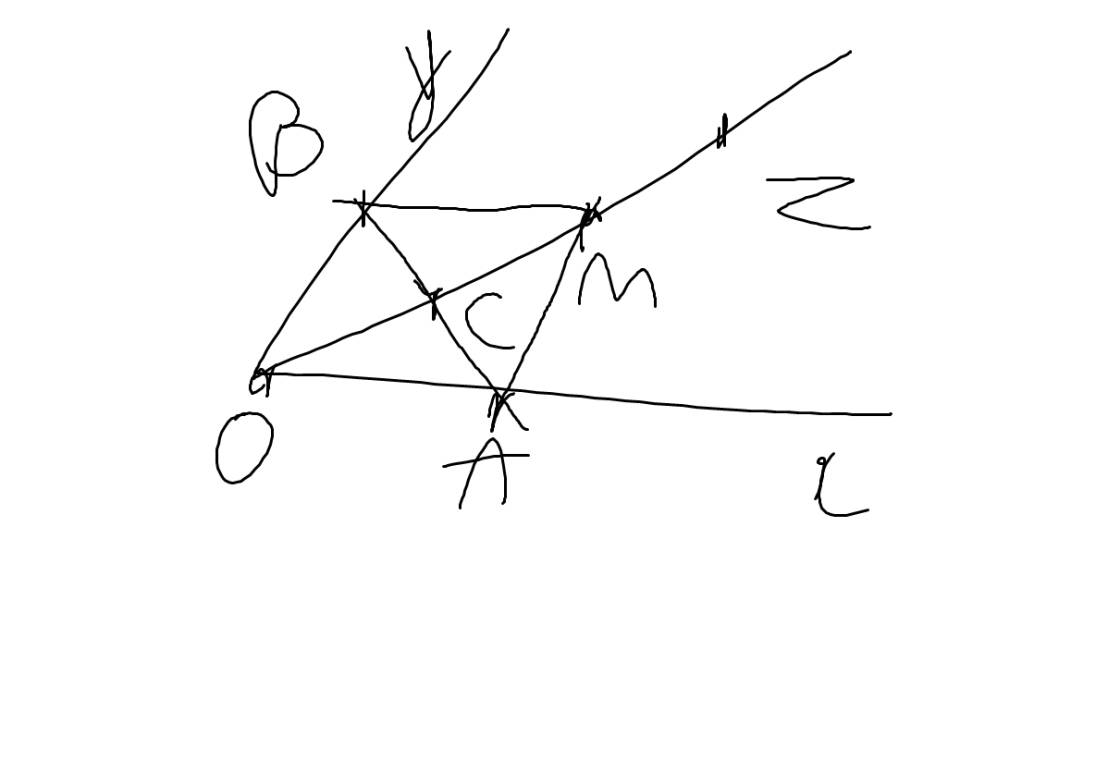

Sửa đề: OA=OB=OC
a: OB là phân giác của góc AOC
=>\(\hat{AOB}=\hat{BOC}=\frac12\cdot\hat{AOC}=60^0\)
Xét ΔOAB có OA=OB và \(\hat{AOB}=60^0\)
nên ΔOAB đều
=>OA=OB=AB và \(\hat{OAB}=\hat{OBA}=\hat{AOB}=60^0\)
Xét ΔOBC có OB=OC và \(\hat{BOC}=60^0\)
nên ΔBOC đều
=>BO=OC=BC và \(\hat{BOC}=\hat{OBC}=\hat{OCB}=60^0\)
Ta có: \(\hat{AOB}=\hat{OBC}\left(=60^0\right)\)
mà hai góc này là hai góc ở vị trí so le trong
nên AO//BC
Ta có: \(\hat{COB}=\hat{ABO}\left(=60^0\right)\)
mà hai góc này là hai góc ở vị trí so le trong
nên OC//AB
b: OA=OB=AB
OB=OC=BC
Do đó: OA=OB=AB=OC=BC
ta có: OA=OC
=>O nằm trên đường trung trực của AC(1)
BA=BC
=>B nằm trên đường trung trực của AC(2)
Từ (1),(2) suy ra OB là đường trung trực của AC
=>OB⊥AC
a: ΔOAB cân tại O
mà OC là phân giác
nên OC vuông góc AB và C là trung điểm của AB
b: Xét tứ giác OAMB có
C là trung điểm chung của OM và AB
=>OAMB là hình bình hành
=>OA//MB và OB//MA