NT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 1 2024
4.
\(\dfrac{x-7}{y-6}=\dfrac{7}{6}\Rightarrow\dfrac{x-7}{7}=\dfrac{y-6}{6}=\dfrac{-y+6}{-6}\)
Áp dụng tính chất dãy tỉ số bằng nhau:
\(\dfrac{x-7}{7}=\dfrac{-y+6}{-6}=\dfrac{x-7-y+6}{7-6}=\dfrac{x-y-1}{1}=-5\)
\(\Rightarrow\left\{{}\begin{matrix}x-7=7.\left(-5\right)=-35\\-y+6=\left(-6\right).\left(-5\right)=30\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=-28\\y=-24\end{matrix}\right.\)
5.
Ta có:
\(A^2=\dfrac{2^2.4^2.6^2...4998^2.5000^2}{3^2.5^2.7^2...4999^2.5001^2}< \dfrac{2^2.4^2.6^2.4998^2.5000^2}{\left(3^2-1\right)\left(5^2-1\right)\left(7^2-1\right)...\left(4999^2-1\right)\left(5001^2-1\right)}\)
\(\Rightarrow A^2< \dfrac{2^2.4^4.6^2...4998^2.5000^2}{2.4.4.6.6.8...4998.5000.5000.5002}=\dfrac{2^2.4^4.6^2...4998^2.5000^2}{2.4^4.6^2...4998^2.5000^2.5002}\)
\(\Rightarrow A^2< \dfrac{2}{5002}=\dfrac{1}{2501}< \dfrac{1}{2500}\)
\(\Rightarrow A< \dfrac{1}{50}\)
\(\Rightarrow A< 0,02\)
NQ
Nguyễn Quốc Đạt
CTVVIP
14 tháng 10 2023
a)
\(175\cdot19+38\cdot175+43\cdot175\\ =175\cdot19+175\cdot38+175\cdot43\\ =175\cdot\left(19+38+43\right)\\ =175\cdot100\\ =17500\)
b)
\(125\cdot75+125\cdot13-80\cdot125\\ =125\cdot75+125\cdot13-125\cdot80\\ =125\cdot\left(75+13-80\right)\\ =125\cdot10\\ =125\cdot8\\ =1000\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
14 tháng 10 2023
a, 175. 19 + 38. 175 + 43. 175
= 175. 19 + 175. 38 + 175. 43
= 175.(19 + 38 + 43)
= 175. 100
= 17500
NM
2
NQ
Nguyễn Quốc Đạt
CTVVIP
5 tháng 12 2023
2/
Xét phân số \(\dfrac{2n-3}{n+1}=\dfrac{2n+2-5}{n+1}=\dfrac{2n+2}{n+1}-\dfrac{5}{n+1}=\dfrac{2\left(n+1\right)}{n+1}-\dfrac{5}{n+1}=2-\dfrac{5}{n+1}\)
\(n\in Z\Rightarrow2n-3\inƯ\left(5\right)=\left\{-1;-5;1;5\right\}\)
Ta có bảng:
| 2n - 3 | -1 | -5 | 1 | 5 |
| n | 1 | -1 | 2 | 4 |
Vậy \(n\in\left\{-1;1;2;4\right\}\)
NQ
Nguyễn Quốc Đạt
CTVVIP
5 tháng 12 2023
1/
(x + 1) + (x + 3) + (x + 5) + ... + (x + 999) = 500
<=> (x + x + x + ... + x) + (1 + 3 + 5 + ... + 999) = 500
Xét tổng A = 1 + 3 + 5 + ... + 999
Số số hạng của A là: (999 - 1) : 2 + 1 = 500
Tổng A là: (999 + 1) x 500 : 2 = 250 000
Do A có 500 số hạng nên có 500 ẩn x.
Vậy ta có: 500x + 250 000 = 500
=> 500x = -249 500
=> x = 499
Vậy x = 499
16 tháng 8
Ta có: \(\frac{A}{10^{10}}=\frac{10^{20}-6}{10^{20}-6\cdot10^{10}}=\frac{10^{20}-6\cdot10^{10}+6\left(10^{10}-1\right)}{10^{20}-6\cdot10^{10}}=1+\frac{6\left(10^{10}-1\right)}{10^{20}-6\cdot10^{10}}\)
\(\frac{B}{10^{10}}=\frac{10^{21}-6}{10^{21}-6\cdot10^{10}}=\frac{10^{21}-6\cdot10^{10}+6\left(10^{10}-1\right)}{10^{21}-6\cdot10^{10}}=1+\frac{6\left(10^{10}-1\right)}{10^{21}-6\cdot10^{10}}\)
Ta có: \(10^{20}<10^{21}\)
=>\(10^{20}-6\cdot10^{10}<10^{21}-6\cdot10^{10}\)
=>\(\frac{6\left(10^{10}-1\right)}{10^{20}-6\cdot10^{10}}>\frac{6\left(10^{10}-1\right)}{10^{21}-6\cdot10^{10}}\)
=>\(\frac{6\left(10^{10}-1\right)}{10^{20}-6\cdot10^{10}}+1>\frac{6\left(10^{10}-1\right)}{10^{21}-6\cdot10^{10}}+1\)
=>\(\frac{A}{10^{10}}>\frac{B}{10^{10}}\)
=>A>B
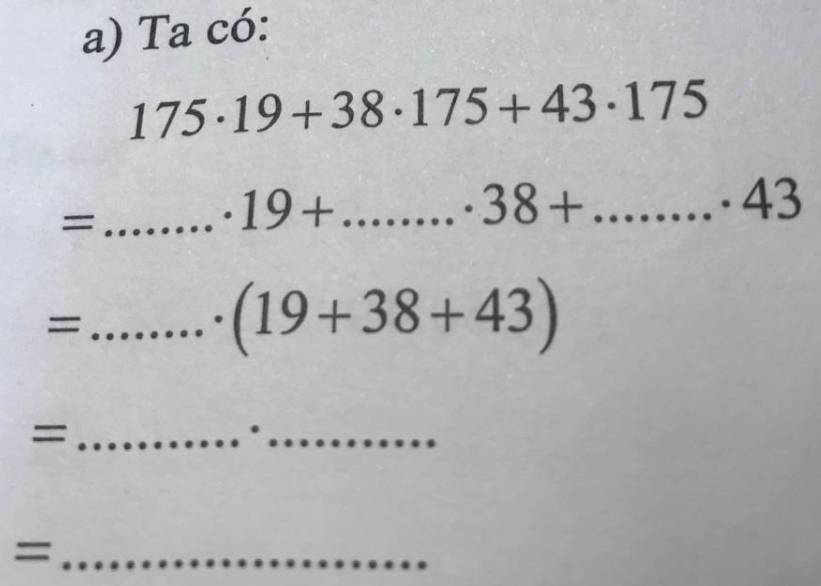
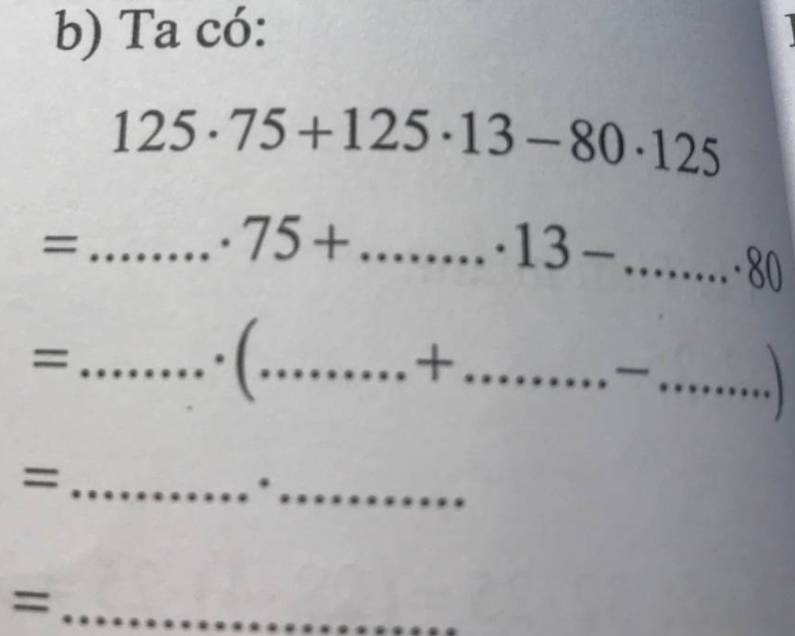
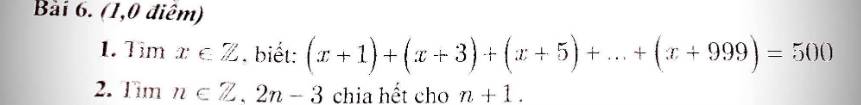
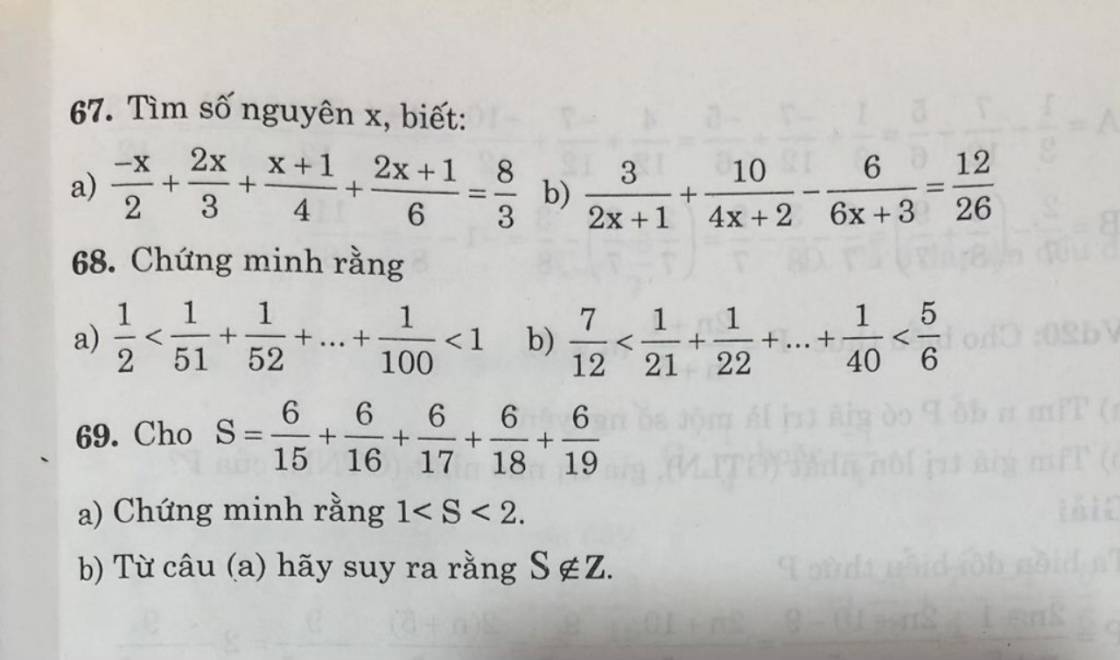
Lời giải:
Dãy trên là dãy cách đều với khoảng cách = 8
Số thứ 110 là: $(110-1)\times 8+144=1016$
Tổng của 110 số hạng đầu tiên:
$(1016+144)\times 110:2=63800$