



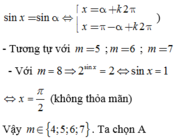
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




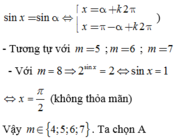

Đáp án A
+)![]() (
(![]() )
)
Điều kiện:![]()
+)![]()
Đặt:![]()
![]()
![]()
![]()
![]()
Đặt![]()
![]() .
.![]()
Bảng biến thiên
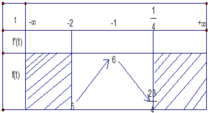
+) ![]()
Để phương trình có hai nghiệm phân biệt![]()
Do đó để phương trình có hai nghiệm phân biệt thì phương trình![]() có nghiệm
có nghiệm![]()
Từ bảng biến thiên![]() .
.

Chọn đáp án D.
![]()
khi đó yêu cầu bài toán trở thành phương trình
f t = 3 t + m
⇔ m = g t = f t - 3 t có nghiệm t ∈ ( 0 ; 1 ] . Có
![]()
Do đó
![]()
![]()
![]()
Vậy - 4 ≤ m < 1
![]()
Tổng các phần tử của tập S bằng -10.

Đáp án D.
Phương trình tương đương với

Đặt 2 x - 1 2 x = t → 4 x + 1 4 x = t 2 + 2 . Xét hàm số t ( x ) = 2 x - 1 2 x trên 0 ; 1 .
Đạo hàm t ' ( x ) = 2 x . ln 2 + ln 2 2 x > 0 , ∀ x ∈ 0 ; 1 ⇒ Hàm số t ( x ) luôn đồng biến trên 0 ; 1 . Suy ra min x ∈ 0 ; 1 t ( x ) = t ( 0 ) = 0 và max x ∈ 0 ; 1 t ( x ) = t ( 1 ) = 3 2 . Như vậy t ∈ 0 ; 3 2 .
Phương trình (1) có dạng:
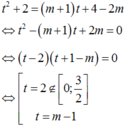
Phương trình (1) có nghiệm t ∈ 0 ; 1 ⇔ phương trình ẩn t có nghiệm t ∈ 0 ; 3 2 ⇔ 0 ≤ m - 1 ≤ 3 2 ⇔ 1 ≤ m ≤ 5 2 . Mà m ∈ ℤ nên m ∈ 1 ; 2 . Tổng tất cả các giá trị nguyên của m bằng 3.

Chọn đáp án C.
Đặt t = sin x ∈ ( 0 ; 1 ] , ∀ x ∈ 0 ; π
Suy ra f sin x = f t ∈ [ - 1 ; 1 ) , ∀ t ∈ ( 0 ; 1 ]
![]()
Vậy phương trình có nghiệm x ∈ 0 ; π ⇔ - 1 < m ≤ 3

Chọn đáp án C.
![]()
Phương trình trở thành: f t = m ( 1 )
Ta cần tìm m để (1) có nghiệm thuộc khoảng ( 0 ; 1 ]
⇔ - 4 ≤ m ≤ - 2