Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABC có
AF,BE,CD là các đường trung tuyến
G là trọng tâm
Do đó: AF,BE,CD đồng quy tại G
Xét tứ giác AGBK có
D là trung điểm chung của AB và KG
=>AGBK là hình bình hành
=>AG//BK và AG=BK
Xét tứ giác AGCH có
E là trung điểm chung của AC và GH
=>AGCH là hình bình hành
=>AG//CH và AG=CH
Ta có: AG//BK
AG//CH
Do đó: BK//CH
ta có: AG=BK
AG=CH
Do đó: BK=CH
Xét tứ giác BKHC có
BK//HC
BK=HC
Do đó: BKHC là hình bình hành
b: Ta có: C,G,D thẳng hàng
G,D,K thẳng hàng
Do đó: C,G,D,K thẳng hàng
=>CK đi qua G
Ta có: B,G,E thẳng hàng
G,E,H thẳng hàng
Do đó: B,G,E,H thẳng hàng
=>BH đi qua G
BCHK là hình bình hành
=>BH cắt CK tại trung điểm của mỗi đường
=>G là trung điểm chung của BH và CK
Hình bình hành BCHK trở thành hình chữ nhật khi KB⊥BC
=>AG⊥BC
=>AF⊥BC
Xét ΔABC có
AF là đường cao
AF là đường trung tuyến
Do đó: ΔABC cân tại A
=>AB=AC

Bài 2:
a: \(\left(-\frac13x^2y\right)\cdot2xy^3=\left(-\frac13\cdot2\right)\cdot x^2\cdot x\cdot y\cdot y^3=-\frac23x^3y^4\)
b: \(\left(-\frac34x^2y\right)\cdot\left(-xy\right)^3=\left(-\frac34\right)\cdot\left(-1\right)\cdot x^2\cdot x^3\cdot y\cdot y^3=\frac34x^5y^4\)
c: \(\frac35\cdot x^2y^5\cdot x^3y^2\cdot\frac{-2}{3}=\left(\frac35\cdot\frac{-2}{3}\right)\cdot x^2\cdot x^3\cdot y^5\cdot y^2=-\frac25x^5y^7\)
d: \(\left(\frac34x^2y^3\right)\cdot\left(2\frac25x^4\right)=\frac34x^2y^3\cdot\frac{12}{5}x^4=\frac34\cdot\frac{12}{5}\cdot x^2\cdot x^4\cdot y^3=\frac95x^6y^3\)
e: \(\left(\frac{12}{15}x^4y^5\right)\cdot\left(\frac59x^2y\right)=\frac45\cdot\frac59\cdot x^4\cdot x^2\cdot y^5\cdot y=\frac49x^6y^6\)
f: \(\left(-\frac17x^2y\right)\left(-\frac{14}{5}x^4y^5\right)=\frac17\cdot\frac{14}{5}\cdot x^2\cdot x^4\cdot y\cdot y^5=\frac25x^6y^6\)
Bài 1: Các đơn thức là \(x^2y;-13;\left(-2\right)^3xy^7\)


a: Xét ΔKAD và ΔBDA có
\(\hat{KAD}=\hat{BDA}\) (hai góc so le trong, AK//BD)
AD chung
\(\hat{KDA}=\hat{BAD}\) (hai góc so le trong, AB//CD)
Do đó: ΔKAD=ΔBDA
=>KA=BD
mà BD=AC
nên AK=AC
=>ΔAKC cân tại A
b: ΔAKC cân tại A
=>\(\hat{AKC}=\hat{ACK}\)
mà \(\hat{AKC}=\hat{BDC}\) (hai góc đồng vị, BD//AK)
nên \(\hat{BDC}=\hat{ACD}\)
Xét ΔBDC va ΔACD có
BD=AC
\(\hat{BDC}=\hat{ACD}\)
CD chung
Do đó: ΔBDC=ΔACD
=>\(\hat{BCD}=\hat{ADC}\)
=>ABCD là hình thang cân

Từ đề bài, ta có hình vẽ sau:
\(\hat{BAC}=\hat{BAH}+\hat{CAH}=10^0+10^0=20^0\)
Xét ΔABC có
AH là đường cao
AH là đường phân giác
Do đó: ΔABC cân tại A
=>\(\hat{ABC}=\frac{180^0-\hat{BAC}}{2}=\frac{180^0-20^0}{2}=80^0\)
Ta có: \(\hat{KBC}+\hat{KBA}=\hat{ABC}\) (tia BK nằm giữa hai tia BA và BC)
=>\(\hat{KBA}=80^0-40^0=40^0\)
Xét ΔABG và ΔACG có
AB=AC
\(\hat{BAG}=\hat{CAG}\)
AG chung
Do đó: ΔABG=ΔACG
=>\(\hat{ABG}=\hat{ACG}\)
=>\(x=40^0\)


Bài 4:
a: \(C=\frac13\left(-6x^2y^2\right)^2\cdot\left(\frac12x^3y\right)=\frac13\cdot36x^4y^4\cdot\frac12x^3y\)
\(=36\cdot\frac13\cdot\frac12\cdot x^4\cdot x^3\cdot y^4\cdot y=6x^7y^5\)
b: Khi x=1;y=-1 thì \(C=6\cdot1^7\cdot\left(-1\right)^5=6\cdot1\cdot\left(-1\right)=-6\)
Bài 3:
\(D=\left(-\frac37x^2y\right)\left(\frac79x^2y^2\right)=-\frac37\cdot\frac79\cdot x^2\cdot x^2\cdot y\cdot y^2=-\frac13x^4y^3\)
hệ số là -1/3
Bậc là 4+3=7
Biến là \(x^4;y^3\)

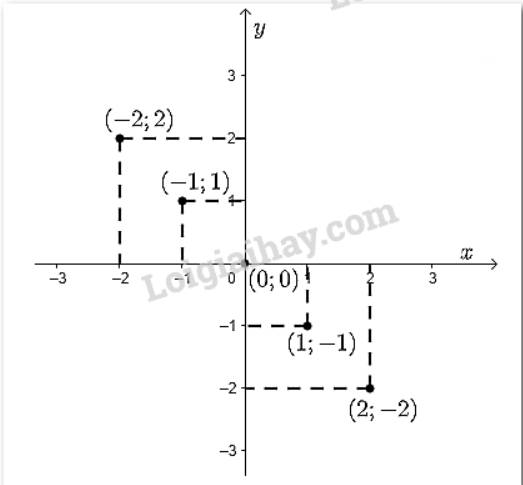
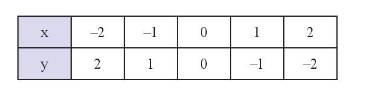
Đồ thị hàm số là tập hợp các điểm có tọa độ \(\left( { - 2;2} \right);\left( { - 1;1} \right);\left( {0;0} \right);\left( {1; - 1} \right);\left( {2; - 2} \right)\) được vẽ trên mặt phẳng tọa độ như hình dưới đây:
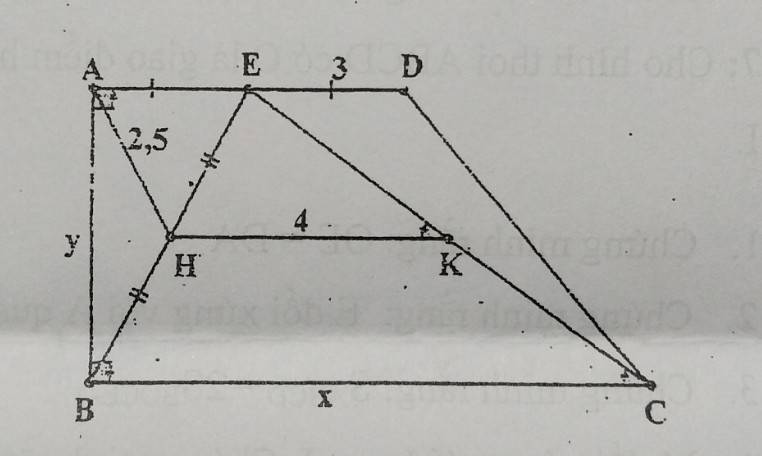









Có: ∠EKH = ∠KCB
Mà 2 góc ở vị trí đồng vị
⇒ HK // BC
Xét △EBC có:
H trung điểm EB
HK // BC
⇒ HK đường trung bình
⇒ HK = \(\dfrac{1}{2}\)BC
⇒ BC = 2HK
⇒ x = 2 . 4 = 8
Xét △AEB ⊥ A, có:
AH đường trung tuyến (H trung điểm EB)
⇒ AH = \(\dfrac{1}{2}\)EB
⇒ EB = 2AH = 2 . 2,5 = 5
Vì AE = ED
Mà ED = 3
⇒ AE = 3
Áp dụng định lý Pytago vào △AEB ⊥ A
⇒ \(EB^2=AE^2+AB^2\)
⇒ AB = y = \(\sqrt{BE^2-AE^2}\) = \(\sqrt{5^2-3^2}\) = \(4\)
Vậy x = 8 và y = 4