GV
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LN
5
LN
3
S
subjects
CTVHS
13 tháng 8
a. áp dụnng định lý pythagore vào △ ABC vuông tại A ta có:
\(BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10\left(\operatorname{cm}\right)\)
b. diện tích △ ABC là:
\(\frac{6\cdot8}{2}=24\left(\operatorname{cm}^2\right)\)
c. ta có: \(BC\cdot AH=AB\cdot AC\)
\(\Rightarrow AH=\frac{AB\cdot AC}{BC}=\frac{6\cdot8}{10}=4,8\left(\operatorname{cm}\right)\)
áp dụng định lý pythagore vào △ ABH vuông tại H ta được:
\(HB=\sqrt{AB^2-AH^2}=\sqrt{6^2-4,8^2}=3,6\left(\operatorname{cm}\right)\)
áp dụng định lý pythagore vào △ AHC vuông tại H ta được:
\(HC=\sqrt{AC^2-AH^2}=\sqrt{8^2-4,8^2}=6,4\left(\operatorname{cm}\right)\)
d. vì M là trung điểm của cạnh BC
⇒ MB = MC = BC : 2 = 10 : 2 = 5 (cm)
ta có: BH + HM = BM
⇒ HM = BM - BH = 5 - 3,6 = 1,4 (cm)
áp dụng định lý pythagore vào △ AHM vuông tại H ta có:
\(AM=\sqrt{AH^2+HM^2}=\sqrt{4,8^2+1,4^2}=5\left(\operatorname{cm}\right)\)
LN
1
13 tháng 8
a: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
=>\(HB=HC=\frac{BC}{2}=\frac{12}{2}=6\left(\operatorname{cm}\right)\)
ΔAHB vuông tại H
=>\(HA^2+HB^2=AB^2\)
=>\(HA^2=10^2-6^2=100-36=64=8^2\)
=>HA=8(cm)
b: Diện tích tam giác ABC là:
\(S_{ABC}=\frac12\cdot AH\cdot BC=\frac12\cdot12\cdot8=4\cdot12=48\left(\operatorname{cm}^2\right)\)
các điểm lưới (cách đều nhau) trong hình vuông được hiển thị trong sơ đồ dưới đây, bao gồm các điểm trên các cạnh. Điểm 
nằm ở trung tâm của hình vuông. Cho rằng điểm đó 
được chọn ngẫu nhiên trong số các 
điểm khác , xác suất để đường thẳng đó 
là đường đối xứng với hình vuông là bao nhiêu?
QN
2 tháng 1 2019
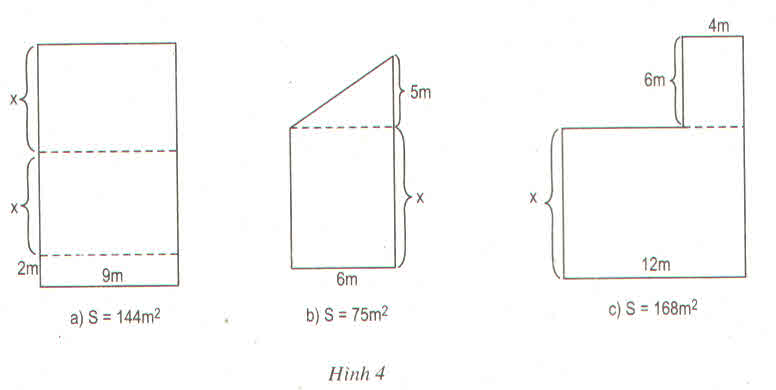
a) 9(2x+2)=144
18x +18=144
18x = 126
x = 7
Vậy x = 7m
b) 6x+15 = 75
6x = 60
x = 10
Vậy x = 10m
c) 12x+24 = 168
12x = 144
x =12
Vậy x = 12m.
17 tháng 5 2022
Ta có: mp(ABCD) // mp(A1B1C1D1)
AB thuộc mp(ABCD)
A1D1 thuộc mp(A1B1C1D1)
AB không song song với A1D1
Vậy mệnh đề đã cho sai.
10 tháng 5 2017
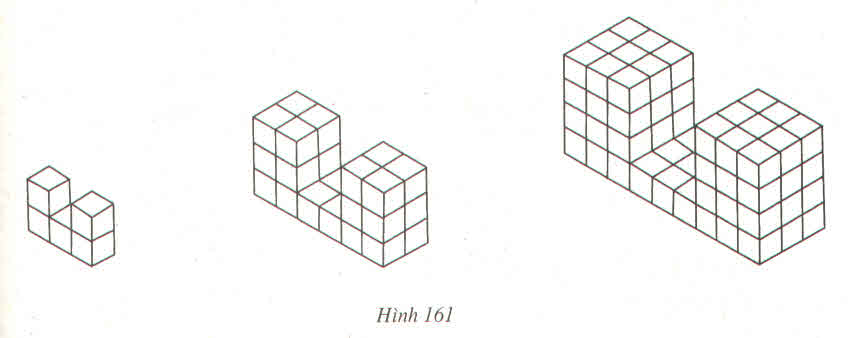
Số hình lập phương ở hình 1: 1.3+1.1.2=5 (khối)
Số hình lập phương ở hình 2:22.3+22.2.2=28 (khối)
Số hình lập phương ở hình 3:32.3+32.3.2=81 (khối)
\(\Rightarrow\)Công tức tính:
Số hình lập phương ở hình x: x2.3+x2.x.2 (khối)
Số hình lập phương ở hình 10 là:102.3+102.10.2=2300 (khối)
5 tháng 7 2017
Cách 1 : Khi ta vẽ hình thứ tư thì :
Số hình lập phương đơn vị ở phía trái là 4.5.4=80
GV
3
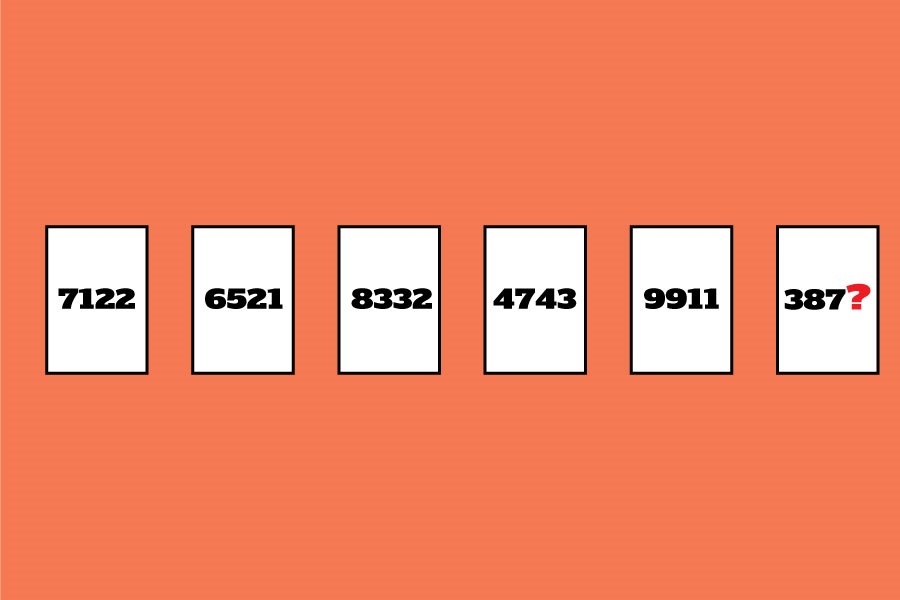
3874 nha
Trả lời: 4. Cộng các chữ số trong mỗi hình, khi bạn di chuyển xuống cột, tổng số này tăng thêm 2 lần, từ 12 đến 22.