Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lăng kính có dạnh hình lăng trụ đứng với đáy là tam giác.

Đèn kéo quân

Hộp sữa có dạng hình lăng trụ đứng tứ giác, cũng là hình hộp chữ nhật.

Viên gạch có dạng hình lăng trụ đứng với đáy là hình lục giác đều


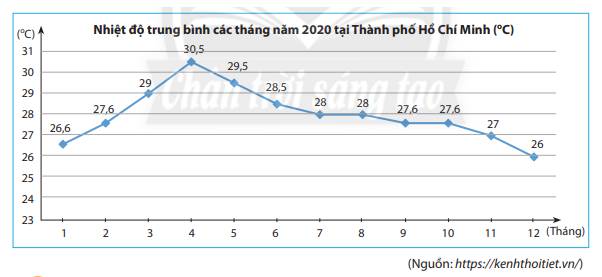
+ Biểu đồ biểu diễn nhiệt độ trung bình các tháng năm 2020 tại Thành phố Hồ Chí Minh.
+ Đơn vị thời gian là tháng, đơn vị số liệu là độ C.
+ Tháng 4 có nhiệt độ trung bình cao nhất.
+ Tháng 12 có nhiệt độ trung bình thấp nhất.
+ Nhiệt độ trung bình tăng trong những khoảng thời gian từ tháng: 1 – 2; 2 – 3; 3 – 4.
+ Nhiệt độ trung bình giảm trong những khoảng thời gian từ tháng: 4 – 5; 5 – 6; 6 – 7; 8 – 9; 10 – 11; 11 – 12.
+ Nhiệt độ trung bình không đổi trong những khoảng thời gian từ tháng: 7 – 8; 9 – 10.

Xét 2 tam giác ABC và MNP có:
AB=MN (gt)
\(\widehat {BAC} = \widehat {NMP}\) (gt)
AC=MP (gt)
Vậy \(\Delta ABC = \Delta MNP\)(c.g.c)

tham khảo
Hình a có dạng kiến trúc hình hộp chữ nhật.
Hình b có dạng kiến trúc hình lập phương.

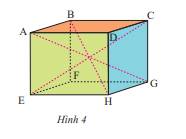
- Các góc ở đỉnh F là: góc BFE, góc BFG, góc EFG
- Các đường chéo được vẽ trong hình là: BH, AG, CE.
- Đường chéo chưa được vẽ là: DF

Em thấy bạn Vuông nói đúng
Để chứng minh điều này, ta có thể chỉ ra trường hợp 2 góc bằng nhau nhưng không đối đỉnh.
Ví dụ:

\(\widehat {{O_1}} = \widehat {{O_2}}\) nhưng hai góc này không đối đỉnh







Hình hộp chữ nhật: Bể cá, viên gạch, tủ lạnh, máy giặt,…
Hình lập phương: Quân xúc xắc, viên đá, cái hộp,…