Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Hai góc có tổng số đo bằng 180 \(^\circ \) không phải là hai góc kề bù, vì 2 góc kề bù phải là 2 góc kề nhau và có tổng số đo bằng 180 \(^\circ \), chẳng hạn:

Góc xOy và góc xOz có tổng số đo bằng 180\(^\circ \) nhưng không phải là hai góc kề bù, vì không kề nhau
b) Hai góc bằng nhau và có chung đỉnh không phải là hai góc đối đỉnh, chẳng hạn:

Góc mAq và nAp bằng nhau và có chung đỉnh nhưng không phải là hai góc đối đỉnh.

a) đúng ví dụ góc đồng vị, góc sole, góc trong cùng phía là những cặp góc bằng nhau
b) Sai vì góc kề bù có tổng số đo là 180 độ vì vậy nó có thể là hai góc vuông
c) Sai vì đó là hai góc bù nhau nhưng không kề nhau vẫn có tổng là 180 độ
d) Sai vì cặp góc kề nhau không đối đỉnh nhau
e) Sai ví dụ như câu trên hai đường thẳng cắt nhau sẽ có hai cặp góc không kề nhau đối đỉnh nhau và một cặp nhọn cặp còn lại tù

Vì AOB và BOC là 2 góc kề bù.
=>AOB+BOC=180
mà BOC=5.AOB
=>AOB+5.AOB=180
=>6.AOB=180
=>AOB=180:6
=>AOB=30(độ)
=>BOC=30.5=150(độ)
Vì 2 góc đối đỉnh có số đo bằng nhau.
=>Góc đối đỉnh của BOC có số đo là 150 độ.

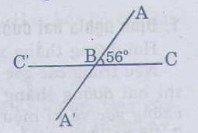
a) Trên hình vẽ bên, ta vẽ góc ˆABC=56∘ABC^=56∘.
b) Vẽ tia đối của tia BC ta được tai BC', được góc ABC' kề bù với góc ABC.
Ta có ˆABC′=180∘−ˆABC=180∘−56∘=124∘ABC′^=180∘−ABC^=180∘−56∘=124∘.
c) Vẽ tia đối của tia BA, ta được tia BA', thì góc C'BA' kề bù với góc ABC'. Ta được ˆC′BA=ˆABCC′BA^=ABC^ (hai góc đối đỉnh) nên ˆC′BA′=56∘.

Câu 1:
A B O M C N
Ta có: Om là tia phân giác của góc AOC => AOm = COm = AOC : 2 (1)
Ta có: COm + COn = mOn
=> COm + COn = 900
Mà: AOm = COm ( chứng minh (1) )
=> AOm + COn = 900 (2)
Ta có: AOm + mOn + BOn = AOB
=> AOm + 900 + BOn = 1800
=> AOm + BOn = 1800 - 900
=> AOm + BOn = 900 (3)
Từ (2) và (3) => COn = BOn
Mà On nằm giữa 2 tia OC và OB
=> On là tia phân giác của góc BOC
Vậy On là tia phân giác của góc BOC.

A B C C' 56 độ A'
b) Ta có:
ABC' kề bù với ABC => ABC' + ABC = 1800
=> ABC' + 560 = 1800 => ABC' = 1800 - 560 = 1240
c) cái đề hơi kì
đúng rồi đấy bạn
Đúng rồi em nhé!