Rút gọn các phân thức: 32 x - 8...

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

PT

Pham Trong Bach

21 tháng 2 2019

Rút gọn các phân thức: 32 x - 8 x 2 + 2 x 3 x 3 + 64

#Hỏi cộng đồng OLM #Toán lớp 8

1

CM

Cao Minh Tâm

21 tháng 2 2019

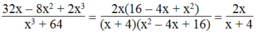
Giải sách bài tập Toán 8 | Giải bài tập Sách bài tập Toán 8

Các câu hỏi dưới đây có thể giống với câu hỏi trên

KW

Karry Wang

5 tháng 6 2017 - olm

rút gọn biểu thức sau :

( 3 + 1 ) x ( 3^2 + 1 ) x ( 3^4 + 1 ) x ( 3^8 +1 ) x ( 3^16 +1 ) x ( 3^32 +1 ) x ( 3^64 +1 )

các bạn giúp mk vs nhé ! cảm ơn nhiều !!!

#Hỏi cộng đồng OLM #Toán lớp 8

1

TQ

Trương Quang Khải

5 tháng 6 2017

Đặt biểu thức đã cho là A.

Ta có: 2A = (3 - 1) * (3 + 1) * (3^2 + 1) * .... * (3^64 + 1)

= (3^2 - 1) * (3^2 + 1) * ... * (3^64 + 1) (hằng đẳng thức a^2 - b^ 2 = (a+b)(a-b))

Rút gọn triệt tiêu ta được 2A=3^64 - 1

=> A = (3^64 - 1)/2

HA

Hoang Anh Vu

23 tháng 7 2017 - olm

rút gọn phân thức

a. \(\frac{x^{32}+x^{16}+1}{x^{16}+x^8+1}\)

b. \(\frac{x^8+3x^4+4}{x^4+x^2+2}\)

#Hỏi cộng đồng OLM #Toán lớp 8

1

LN

Le Nhat Phuong

23 tháng 7 2017

a, \(\frac{x^{32}+x^{16}+1}{x^{16}+x^8+1}\)

\(=\frac{x^8+x^4+1}{x^4+x^2+1}\) Vậy phân thức \(a=\frac{x^8+x^4+1}{x^4+x^2+1}\)

P/s; Căn thức a, là phân số tối giản

b, \(\frac{x^8+3x^4+4}{x^4+x^2+2}\)

\(=\frac{x^4+3x^2+2}{x^2+x^1+1}\) Vậy căn thức \(b=\frac{x^4+3x^2+2}{x^2+x^1+1}\)

P/s; Căn thức b, có thể rút gọn được cho 2 và 4

Em ko chắc đâu nhé *-*

KJ

Kwon Ji Jong

29 tháng 6 2017 - olm

Rút gọn phân thức

a)\(\frac{9-\left(x+5\right)^2}{x^2+4x+4}\)

b)\(\frac{32x-8x+2x^3}{x^3+64}\) . Giúp mk nha,mk tik cho .

#Hỏi cộng đồng OLM #Toán lớp 8

1

TT

tran thanh ngoc

29 tháng 6 2017

khó qua mik mới hc lớp 7 thôi

HA

Hoang Anh Vu

12 tháng 7 2017 - olm

rút gọn phân thức:

a, \(\frac{32x-8x^2+2x^3}{x^3+64}\)

giúp mình vs nào

#Hỏi cộng đồng OLM #Toán lớp 8

1

HT

Hoàng Thị Lan Hương

12 tháng 7 2017

Ta có \(\frac{32x-8x^2+2x^3}{x^3+64}=\frac{x\left(32-8x+2x^2\right)}{\left(x+4\right)\left(x^2-4x+16\right)}=\frac{2x\left(x^2-4x+16\right)}{\left(x+4\right)\left(x^2-4x+16\right)}=\frac{2x}{x+4}\)

PJ

Park Jimin - Mai Thanh Hoa

8 tháng 8 2017 - olm

Rút gọn các phân thức sau :

a) \(\frac{80x^2-125x}{3\left(x-3\right)-\left(x-3\right)\left(8-4x\right)}\)

b) \(\frac{9-\left(x+5\right)^2}{x^2+4x+4}\)

Help me !

#Hỏi cộng đồng OLM #Toán lớp 8

2

HH

hoàng hồng hoa

8 tháng 8 2017

phân tích thành nhân tử ở mẫu và tử sau đó ta rút gọn vậy là ra đáp số

PJ

Park Jimin - Mai Thanh Hoa

8 tháng 8 2017

a) \(=\frac{5x\left(16x^2-25\right)}{\left(x-3\right)\left(4x-5\right)}\)\(\)

\(=\frac{5x\cdot\left(4x-5\right)\left(4x+5\right)}{\left(x-3\right)\left(4x-5\right)}\)

\(=\frac{5x\left(4x+5\right)}{x-3}\)

b) \(=\frac{3^2-\left(x+5\right)^2}{\left(x+2\right)^2}\)

\(=\frac{\left(3-x-5\right)\left(3+x+5\right)}{\left(x+2\right)^2}\)

\(=\frac{\left(x+2\right)\left(8+x\right)}{\left(x+2\right)^2}\)

\(=\frac{8+x}{x+2}\)

UN

Uyển Nhi Trần

24 tháng 12 2017 - olm

Bài 1: Rút gọn phân thức

a) \({36 ({x-2})^3 \over 32-16x}\)

#Hỏi cộng đồng OLM #Toán lớp 8

0

CN

Cấn Ngọc Minh

18 tháng 10 2020 - olm

1.Rút gọn rồi tính giá trị của biểu thức sau thành nhân tử
B= \(\left(x-2\right)\left(x+2\right)\left(x+3\right)-\left(x+1\right)^3\)

2.Phân tích đa thức sau thành nhân tử

\(64-x^2-y^2+2xy\)

3. Tìm x

\(2x^3-x^2+2x-1=0\)

#Hỏi cộng đồng OLM #Toán lớp 8

4

NN

Nobi Nobita

18 tháng 10 2020

1. \(B=\left(x-2\right)\left(x+2\right)\left(x+3\right)-\left(x+1\right)^3\)

\(=\left(x^2-4\right)\left(x+3\right)-\left(x^3+3x^2+3x+1\right)\)

\(=x^3+3x^2-4x-12-x^3-3x^2-3x-1\)

\(=-7x-13\)

2. \(64-x^2-y^2+2xy=64-\left(x^2+y^2-2xy\right)\)

\(=64-\left(x-y\right)^2=\left(8+x-y\right)\left(8-x+y\right)\)

3. \(2x^3-x^2+2x-1=0\)

\(\Leftrightarrow x^2.\left(2x-1\right)+\left(2x-1\right)=0\)

\(\Leftrightarrow\left(2x-1\right)\left(x^2+1\right)=0\)

Vì \(x^2\ge0\)\(\Rightarrow x^2+1>0\)

\(\Rightarrow2x-1=0\)\(\Rightarrow2x=1\)\(\Rightarrow x=\frac{1}{2}\)

Vậy \(x=\frac{1}{2}\)

LD

l҉o҉n҉g҉ d҉z҉

18 tháng 10 2020

Bài 1.

B = ( x - 2 )( x + 2 )( x + 3 ) - ( x + 1 )³

= ( x² - 4 )( x + 3 ) - ( x³ + 3x² + 3x + 1 )

= x³ + 3x² - 4x - 12 - x³ - 3x² - 3x - 1

= -7x - 13

Bài 2.

64 - x² - y² + 2xy

= 64 - ( x² - 2xy + y² )

= 8² - ( x - y )²

= ( 8 - x + y )( 8 + x - y )

Bài 3.

2x³ - x² + 2x - 1 = 0

<=> ( 2x³ - x² ) + ( 2x - 1 ) = 0

<=> x²( 2x - 1 ) + 1( 2x - 1 ) = 0

<=> ( 2x - 1 )( x² + 1 ) = 0

<=> \(\orbr{\begin{cases}2x-1=0\\x^2+1=0\end{cases}}\Leftrightarrow x=\frac{1}{2}\)( vì x² + 1 ≥ 1 > 0 ∀ x )

TN

Tuyết Như Bùi Thân

4 tháng 7 2023

Rút gọn các biểu thức sau

1. (x + 1) ^ 3 - (x - 4)(x + 4) - x ^ 3

2. (x + 2) ^ 3 - x(x + 3)(x - 3) - 12x ^ 2 - 8

#Hỏi cộng đồng OLM #Toán lớp 8

2

H9

HT.Phong (9A5)

4 tháng 7 2023

1) \(\left(x+1\right)^3-\left(x-4\right)\left(x+4\right)-x^3\)

\(=\left(x^3+3x^2+3x+1\right)-\left(x^2-16\right)-x^3\)

\(=x^3+3x^2+3x+1-x^2+16-x^3\)

\(=2x^2+3x+17\)

2) \(\left(x+2\right)^3-x\left(x+3\right)\left(x-3\right)-12x^2-8\)

\(=\left(x^3+6x^2+12x+8\right)-x\left(x^2-9\right)-12x^2-8\)

\(=x^3+6x^2+12x+8-x^3+9x-12x^2-8\)

\(=-6x^2+21x\)

KT

『Kuroba ム Tsuki Ryoo ︵²ᵏ⁷』

4 tháng 7 2023

`@` `\text {Ans}`

`\downarrow`

`1.`

\((x + 1) ^ 3 - (x - 4)(x + 4) - x ^ 3\)

`= x^3 + 3x^2 + 3x + 1 - [ x(x+4) - 4(x+4)] - x^3`

`= x^3 + 3x^2 + 3x + 1 - (x^2 + 4x - 4x - 16) - x^3`

`= x^3 + 3x^2 + 3x + 1 - (x^2 - 16) - x^3`

`= x^3 + 3x^2 + 3x + 1 - x^2 + 16 - x^3`

`= (x^3 - x^3) + (3x^2 - x^2) + 3x + (1+16)`

`= 2x^2 + 3x + 17`

`2.`

\((x + 2) ^ 3 - x(x + 3)(x - 3) - 12x ^ 2 - 8\)

`= x^3 + 6x^2 + 12x + 8 - [ (x^2 + 3x)(x-3)] - 12x^2 - 8`

`= x^3 + 6x^2 + 12x + 8 - (x^3 - 9x) - 12x^2 - 8`

`= x^3 + 6x^2 + 12x +8 - x^3 + 9x - 12x^2 - 8`

`= (x^3 - x^3) + (6x^2 - 12x^2) + (12x + 9x) + (8-8)`

`= -6x^2 + 21x `

TC

TFBOYS CUTE

24 tháng 5 2017 - olm

rút gọn biểu thức sau :

( 3 + 1 ) x ( 3^2 + 1 ) x ( 3^4 + 1 ) x ( 3^8 + 1 ) x ( 3^16 + 1 ) x ( 3^32 + 1 ) x ( 3^64 + 1 )

MN ƠI ! GIÚP MK NHA !!! MK CẢM ƠN MN THẬT NHIỀU ~

#Hỏi cộng đồng OLM #Toán lớp 8

3

DH

Dương Huy Vũ

24 tháng 5 2017

à bài này dễ mà

đầu tiên nhá:không biết,tiếp theo:ko biết.Thế thôi còn lại bạn tự giải

VL

Vũ Lê Hiểu Khanh

9 tháng 7 2017

bạn sử dụng hằng đẳng thức nhé .Mình bít nhg lười viết nắm

HB

Hải Băng

14 tháng 1 2016 - olm

\(A=\left(x^2-x+1\right)\left(x^4-x^2+1\right)\left(x^8-x^4+1\right)\left(x^{16}-x^8+1\right)\left(x^{32}-x^{16}+1\right)\)

Rút gọn A dưới dạng phân thức

#Hỏi cộng đồng OLM #Toán lớp 8

1

TN

Thắng Nguyễn

14 tháng 1 2016

-x^61+5*x^60+x^59-5*x^58-x^55+5*x^54+x^53-5*x^52-x^49+5*x^48+x^47-5*x^46x^43+5*x^42+x^41-5*x^40-x^37+5*x^36+x^35-5*x^34-x^49+5*x^48+x^47-5*x^46x^43+5*x^42+x^41-5*x^40-x^37+5*x^36+x^35-5*x^34-x^31+5*x^30+x^27-5*x^26-x^25+5*x^24+x^21-5*x^20-x^19+5*x^18+x^15-5*x^14-x^13+5*x^12+x^9-5*x^8-x^7+5*x^6+x^3-5*x^2-x+5