Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a. Câu này đơn giản em tự giải
b.
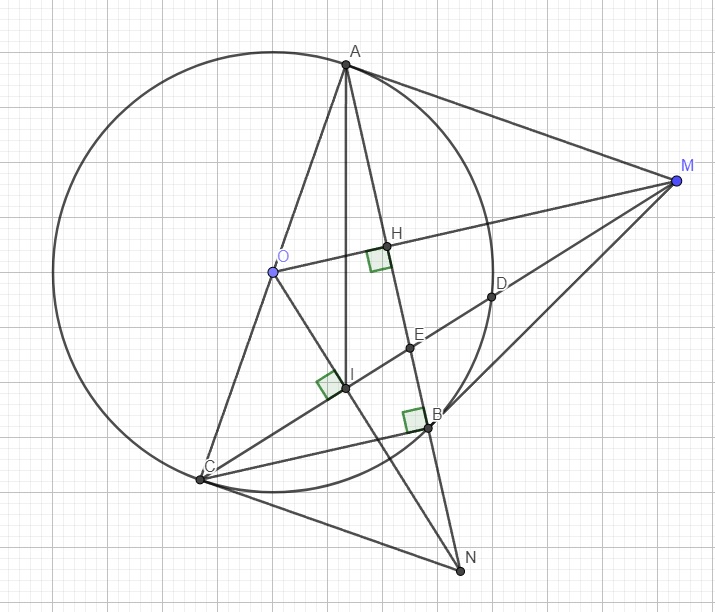
Xét hai tam giác OIM và OHN có:
\(\left\{{}\begin{matrix}\widehat{OIM}=\widehat{OHN}=90^0\\\widehat{MON}\text{ chung}\\\end{matrix}\right.\) \(\Rightarrow\Delta OIM\sim\Delta OHN\left(g.g\right)\)
\(\Rightarrow\dfrac{OI}{OH}=\dfrac{OM}{ON}\Rightarrow OI.ON=OH.OM\)
Cũng từ 2 tam giác đồng dạng ta suy ra \(\widehat{OMI}=\widehat{ONH}\)
Tứ giác OAMI nội tiếp (I và A cùng nhìn OM dưới 1 góc vuông)
\(\Rightarrow\widehat{OAI}=\widehat{OMI}\)
\(\Rightarrow\widehat{OAI}=\widehat{ONH}\) hay \(\widehat{OAI}=\widehat{ONA}\)
c.
Xét hai tam giác OAI và ONA có:
\(\left\{{}\begin{matrix}\widehat{OAI}=\widehat{ONA}\left(cmt\right)\\\widehat{AON}\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta OAI\sim\Delta ONA\left(g.g\right)\)
\(\Rightarrow\dfrac{OA}{ON}=\dfrac{OI}{OA}\Rightarrow OI.ON=OA^2=OC^2\) (do \(OA=OC=R\))
\(\Rightarrow\dfrac{OC}{ON}=\dfrac{OI}{OC}\)
Xét hai tam giác OCN và OIC có:
\(\left\{{}\begin{matrix}\dfrac{OC}{ON}=\dfrac{OI}{OC}\\\widehat{CON}\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta OCN\sim\Delta OIC\left(g.g\right)\)
\(\Rightarrow\widehat{OCN}=\widehat{OIC}=90^0\) hay tam giác ACN vuông tại C
\(\widehat{ABC}\) là góc nt chắn nửa đường tròn \(\Rightarrow BC\perp AB\)
Áp dụng hệ thức lượng trong tam giác vuông ACN với đường cao BC:
\(BC^2=BN.BA=BN.2BH=2BN.BH\) (1)
O là trung điểm AC, H là trung điểm AB \(\Rightarrow OH\) là đường trung bình tam giác ABC
\(\Rightarrow OH=\dfrac{1}{2}BC\)
Xét hai tam giác OHN và EBC có:
\(\left\{{}\begin{matrix}\widehat{OHN}=\widehat{EBC}=90^0\\\widehat{ONH}=\widehat{ECB}\left(\text{cùng phụ }\widehat{IEB}\right)\end{matrix}\right.\) \(\Rightarrow\Delta OHN\sim\Delta EBC\left(g.g\right)\)
\(\Rightarrow\dfrac{OH}{EB}=\dfrac{HN}{BC}\Rightarrow HN.EB=OH.BC=\dfrac{1}{2}BC^2\)
\(\Rightarrow BC^2=2HN.EB\) (2)
(1);(2) \(\Rightarrow BN.BH=HN.BE\)
\(\Rightarrow BN.BH=\left(BN+BH\right).BE\)
\(\Rightarrow\dfrac{1}{BE}=\dfrac{BN+BH}{BN.BH}=\dfrac{1}{BH}+\dfrac{1}{BN}\) (đpcm)


a: Diện tích ban đầu là \(8\cdot20=160\left(m^2\right)\)
Độ dài cạnh góc vuông thứ nhất của phần bị thu hồi là
20-2x(m)
Độ dài cạnh góc vuông thứ hai của phần bị thu hồi là:
8-x(m)
Diện tích phần bị thu hồi là:
\(T=\frac12\left(20-2x\right)\left(8-x\right)=\frac12\left(2x-20\right)\left(x-8\right)=\left(x-10\right)\left(x-8\right)\left(m^2\right)\)
b: Diện tích đất bị thu hồi là 455:13=35(m)
=>(x-10)(x-8)=35
=>\(x^2-18x+80-35=0\)
=>\(x^2-18x+45=0\)
=>(x-3)(x-15)=0
=>\(\left[\begin{array}{l}x-3=0\\ x-15=0\end{array}\right.\Rightarrow\left[\begin{array}{l}x=3\left(nhận\right)\\ x=15\left(loại\right)\end{array}\right.\)
Vậy: x=3

Ta có:
\(x^4+4=\left(x^4+4x^2+4\right)-4x^2\)
=\(\left(x^2+2\right)^2-\left(2x\right)^2=\left(x^2+2x+2\right)\left(x^2-2x+2\right)\)
=> \(x^4+4\) chia hết cho \(x^2+2x+a\) khi \(\left(x^2+2x+2\right)\left(x^2-2x+2\right)⋮\left(x^2+2x+a\right)\)
=> a = 2.

Xét một phân số trong tổng:
\(\frac{1}{\sqrt{k} + \sqrt{k + 1}}\)
Nhân cả tử và mẫu với \(\sqrt{k + 1} - \sqrt{k}\), ta được:
\(\frac{1}{\sqrt{k} + \sqrt{k + 1}} = \frac{\sqrt{k + 1} - \sqrt{k}}{\left(\right. \sqrt{k} + \sqrt{k + 1} \left.\right) \left(\right. \sqrt{k + 1} - \sqrt{k} \left.\right)} = \sqrt{k + 1} - \sqrt{k}\)
Vậy:
\(A=\left(\right.\sqrt{2}-\sqrt{1}\left.\right)+\left(\right.\sqrt{3}-\sqrt{2}\left.\right)+\cdots+\left(\right.\sqrt{n + 1}-\sqrt{n}\left.\right)\)
Cộng các hạng tử lại, ta thấy \(\sqrt{2}\) ở số hạng đầu bị trừ đi ở số hạng sau, \(\sqrt{3}\) cũng vậy,… chỉ còn:
\(A = \sqrt{n + 1} - \sqrt{1} = \sqrt{n + 1} - 1\)
Đáp số: \(\sqrt{n + 1} - 1\)
Tham khảo

goi V la` can bac hai , abs la` gia tri tuyet doi
ta co P=V((x^3+3)^2/x^2) + V(x-2)^2 =abs((x^3+3)/x)+abs(x-2)
do x thuoc Z nen abs(x-2) thuoc Z
vay de~ P thuoc Z thi` (x^3+3) chia het cho x
=>x thuoc uoc cua 3
=>X={-3;-1;1;3} =>S={5;11;13}

a: Xét (HA/2) có
ΔAEH nội tiếp
AH là đường kính
Do đó: ΔAEH vuông tại E
=>HE⊥AB tại E
Xét (HA/2) có
ΔAFH nội tiếp
AH là đường kính
Do đó: ΔAFH vuông tại F
=>HF⊥AC tại F
Xét ΔAHB vuông tại H có HE là đường cao
nên \(AE\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HF là đường cao
nên \(AF\cdot AC=AH^2\left(2\right)\)
Từ (1),(2) suy ra \(AE\cdot AB=AF\cdot AC=AH^2\)
Ta có: \(AE\cdot AB=AF\cdot AC\)
=>\(\frac{AE}{AC}=\frac{AF}{AB}\)
Xét ΔAEF vuông tại A và ΔACB vuông tại A có
\(\frac{AE}{AC}=\frac{AF}{AB}\)
Do đó: ΔAEF~ΔACB
b: Xét tứ giác AEHF có \(\hat{AEH}=\hat{AFH}=\hat{FAE}=90^0\)
nên AEHF là hình chữ nhật
=>\(\hat{AFE}=\hat{AHE}\)
mà \(\hat{AHE}=\hat{ABC}\left(=90^0-\hat{HAB}\right)\)
nên \(\hat{AFE}=\hat{ABC}\)
ΔOAC cân tại O
=>\(\hat{OAC}=\hat{OCA}=\hat{ACB}\)
\(\hat{AFE}+\hat{OAC}=\hat{ABC}+\hat{ACB}=90^0\)
=>AO⊥ FE
c: Xét (O) có
ΔAKH nội tiếp
AH là đường kính
Do đó: ΔAKH vuông tại K
=>HK⊥AT tại K
Xét ΔAHT vuông tại H có HK là đường cao
nên \(AK\cdot AT=AH^2\)
=>\(AK\cdot AT=AE\cdot AB\)
=>\(\frac{AK}{AE}=\frac{AB}{AT}\)
Xét ΔAKB và ΔAET có
\(\frac{AK}{AE}=\frac{AB}{AT}\)
góc KAB chung
Do đó: ΔAKB~ΔAET
=>\(\hat{AKB}=\hat{AET}\)
d: ta có: A,C,B,K cùng thuộc (O)
=>ACBK nội tiếp
=>\(\hat{ACB}+\hat{AKB}=180^0\)
mà \(\hat{AKB}+\hat{AKI}=180^0\) (hai góc kề bù)
nên \(\hat{IKA}=\hat{ICB}\)
Xét ΔIKA và ΔICB có
\(\hat{IKA}=\hat{ICB}\)
góc KIA chung
Do đó: ΔIKA~ΔICB







Hehêhe giữ lời thì tảnh ảnh đẹp đấy nha
sao ko dăng nhìu nhìu nhìn cho đx
sao nhìn giống ảnh mạng vậy