Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

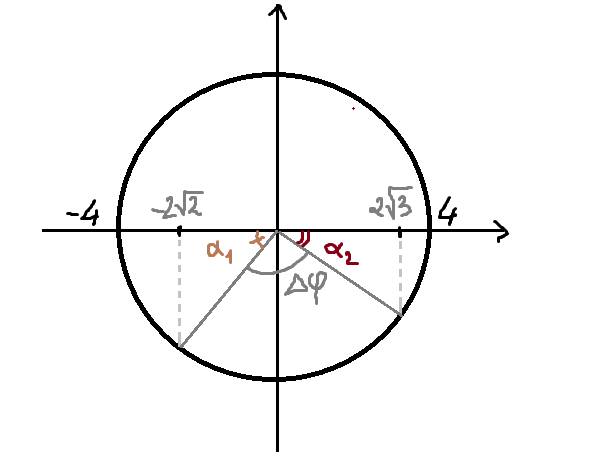
Ta có : \(A=4cm\)
\(cos\alpha_1=\dfrac{-2\sqrt{2}}{4}=-\dfrac{\sqrt{2}}{2}\Rightarrow\alpha_1=\dfrac{3\pi}{4}rad\)
\(cos\alpha_2=\dfrac{2\sqrt{3}}{4}=\dfrac{\sqrt{3}}{2}\Rightarrow\alpha_2=\dfrac{\pi}{6}rad\)
\(\Delta\varphi=\left(\dfrac{\pi}{2}-\dfrac{3\pi}{4}\right)+\left(\dfrac{\pi}{2}-\dfrac{\pi}{6}\right)=\dfrac{\pi}{12}rad\)
Có : \(T=\dfrac{2\pi}{\omega}=\dfrac{2\pi}{\pi}=2s\)
\(\Delta t=\dfrac{\Delta\varphi}{2\pi}.T=\dfrac{\dfrac{\pi}{12}}{2\pi}.2=\dfrac{1}{12}s\)
Vậy ...
Hình ảnh biểu diễn :

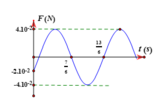
Từ phương trình \(x = 5 sin \left(\right. 2 \pi t + \frac{\pi}{6} \left.\right)\) (cm)
\(\Rightarrow A = 5\) cm; \(\omega = 2 \pi\) rad/s
Ta có: \(\text{v} = x^{'} = \omega A cos \left(\right. \omega t + \varphi \left.\right) = 2 \pi . 5. cos \left(\right. 2 \pi t + \frac{\pi}{6} \left.\right) = 10 \pi cos \left(\right. 2 \pi t + \frac{\pi}{6} \left.\right)\) cm/s
a. Ở thời điểm \(t = 5\) s
Ta có: \(x = 5 sin \left(\right. 2 \pi . 5 + \frac{\pi}{6} \left.\right) = 2 , 5\) cm
\(\text{v} = 10 \pi cos \left(\right. 2 \pi . 5 + \frac{\pi}{6} \left.\right) = 5 \sqrt{30}\) cm/s
\(a = - \omega^{2} x = - \left(\left(\right. 2 \pi \left.\right)\right)^{2} . 2 , 5 = - 100\) cm/s2
b. Khi pha dao động là 120o.
\(x = 5 sin 12 0^{o} = 2 , 5 \sqrt{3}\) cm
\(v = 10 \pi cos 12 0^{o} = - 5 \pi\) cm/s
\(a = - \omega^{2} x = - 4 \pi^{2} . 2 , 5 \sqrt{3} = - \sqrt{3}\) cm/s2

Ta có phương trình dao động điều hòa của vật:
\(x = 8 cos \left(\right. 5 \pi t + \frac{\pi}{3} \left.\right)\)
Trong đó:
- \(x\) là vị trí của vật (đơn vị cm),
- \(t\) là thời gian (đơn vị s),
- \(8\) là biên độ dao động (đơn vị cm),
- \(5 \pi\) là tần số góc (rad/s),
- \(\frac{\pi}{3}\) là pha ban đầu.
Chúng ta sẽ lần lượt giải quyết từng câu hỏi.
a. Xác định trạng thái đầu
Trạng thái đầu của vật là trạng thái tại thời điểm \(t = 0\).
Thay \(t = 0\) vào phương trình dao động:
\(x \left(\right. 0 \left.\right) = 8 cos \left(\right. 5 \pi \times 0 + \frac{\pi}{3} \left.\right) = 8 cos \left(\right. \frac{\pi}{3} \left.\right)\)
Biết rằng \(cos \left(\right. \frac{\pi}{3} \left.\right) = \frac{1}{2}\), ta có:
\(x \left(\right. 0 \left.\right) = 8 \times \frac{1}{2} = 4 \textrm{ } \text{cm}\)
Vậy, trạng thái đầu của vật là \(x = 4 \textrm{ } \text{cm}\).
b. Xác định thời điểm lần đầu vật đạt vị trí biên dương
Vị trí biên dương là giá trị cực đại của \(x\), tức là khi \(x = 8 \textrm{ } \text{cm}\) (biên độ dao động).
Ta cần tìm thời điểm \(t\) sao cho:
\(8 cos \left(\right. 5 \pi t + \frac{\pi}{3} \left.\right) = 8\)
Chia hai vế cho 8:
\(cos \left(\right. 5 \pi t + \frac{\pi}{3} \left.\right) = 1\)
Giải phương trình:
\(5 \pi t + \frac{\pi}{3} = 2 k \pi \text{v}ớ\text{i} \textrm{ } k \in \mathbb{Z}\)
Giải phương trình trên:
\(5 \pi t = 2 k \pi - \frac{\pi}{3}\)
Chia cả hai vế cho \(5 \pi\):
\(t = \frac{2 k \pi - \frac{\pi}{3}}{5 \pi} = \frac{2 k - \frac{1}{3}}{5}\)
Khi \(k = 0\), ta có:
\(t = \frac{- \frac{1}{3}}{5} = - \frac{1}{15} \textrm{ } \text{s}\)
Vì thời gian phải dương, ta chọn \(k = 1\):
\(t = \frac{2 - \frac{1}{3}}{5} = \frac{\frac{5}{3}}{5} = \frac{1}{3} \textrm{ } \text{s}\)
Vậy, thời điểm lần đầu vật đạt vị trí biên dương là \(t = \frac{1}{3} \textrm{ } \text{s}\).
c. Xác định thời điểm lần đầu vật qua vị trí cân bằng
Vị trí cân bằng là \(x = 0\), tức là khi \(cos \left(\right. 5 \pi t + \frac{\pi}{3} \left.\right) = 0\).
Ta giải phương trình:
\(cos \left(\right. 5 \pi t + \frac{\pi}{3} \left.\right) = 0\)
Điều này xảy ra khi:
\(5 \pi t + \frac{\pi}{3} = \frac{\pi}{2} + k \pi \text{v}ớ\text{i} \textrm{ } k \in \mathbb{Z}\)
Giải phương trình:
\(5 \pi t = \frac{\pi}{2} + k \pi - \frac{\pi}{3}\)
Tính toán:
\(5 \pi t = \frac{\pi}{6} + k \pi\)
Chia cả hai vế cho \(5 \pi\):
\(t = \frac{\frac{\pi}{6} + k \pi}{5 \pi} = \frac{1}{30} + \frac{k}{5}\)
Khi \(k = 0\), ta có:
\(t = \frac{1}{30} \textrm{ } \text{s}\)
Vậy, thời điểm lần đầu vật qua vị trí cân bằng là \(t = \frac{1}{30} \textrm{ } \text{s}\).
d. Xác định thời điểm lần thứ 5 vật qua vị trí \(x = - 4 \textrm{ } \text{cm}\), với \(v > 0\)
Vị trí \(x = - 4 \textrm{ } \text{cm}\) ứng với phương trình:
\(- 4 = 8 cos \left(\right. 5 \pi t + \frac{\pi}{3} \left.\right)\)
Chia hai vế cho 8:
\(- \frac{1}{2} = cos \left(\right. 5 \pi t + \frac{\pi}{3} \left.\right)\)
Giải phương trình:
\(5 \pi t + \frac{\pi}{3} = \pi - \frac{\pi}{3} + 2 k \pi \text{v}ớ\text{i} \textrm{ } k \in \mathbb{Z}\)
Tính toán:
\(5 \pi t + \frac{\pi}{3} = \frac{2 \pi}{3} + 2 k \pi\)\(5 \pi t = \frac{2 \pi}{3} + 2 k \pi - \frac{\pi}{3} = \frac{\pi}{3} + 2 k \pi\)
Chia cả hai vế cho \(5 \pi\):
\(t = \frac{\frac{\pi}{3} + 2 k \pi}{5 \pi} = \frac{1}{15} + \frac{2 k}{5}\)
Vậy:
\(t_{1} = \frac{1}{15} \textrm{ } \text{s} \left(\right. k = 0 \left.\right)\)\(t_{2} = \frac{7}{15} \textrm{ } \text{s} \left(\right. k = 1 \left.\right)\)\(t_{3} = \frac{13}{15} \textrm{ } \text{s} \left(\right. k = 2 \left.\right)\)\(t_{4} = \frac{19}{15} \textrm{ } \text{s} \left(\right. k = 3 \left.\right)\)\(t_{5} = \frac{25}{15} = \frac{5}{3} \textrm{ } \text{s} \left(\right. k = 4 \left.\right)\)
Vậy, thời điểm lần thứ 5 vật qua vị trí \(x = - 4 \textrm{ } \text{cm}\) với \(v > 0\) là \(t = \frac{5}{3} \textrm{ } \text{s}\).
Tóm tắt:
- a. Trạng thái đầu: \(x = 4 \textrm{ } \text{cm}\)
- b. Thời điểm lần đầu vật đạt vị trí biên dương: \(t = \frac{1}{3} \textrm{ } \text{s}\)
- c. Thời điểm lần đầu vật qua vị trí cân bằng: \(t = \frac{1}{30} \textrm{ } \text{s}\)
- d. Thời điểm lần thứ 5 vật qua vị trí \(x = - 4 \textrm{ } \text{cm}\) với \(v > 0\): \(t = \frac{5}{3} \textrm{ } \text{s}\)

\(L=12cm\Rightarrow A=\dfrac{L}{2}=6cm\)
Chu kì dao động: \(T=\dfrac{62,8}{20}=3,14s\approx\pi\left(s\right)\Rightarrow\omega=\dfrac{2\pi}{T}=2\)
Áp dụng pt độc lập: \(x^2+\dfrac{v^2}{\omega^2}=A^2\)
\(\Rightarrow\left(-2\right)^2+\dfrac{v^2}{2^2}=6^2\Rightarrow v=\pm8\sqrt{2}\left(cm/s\right)=\pm0,08\sqrt{2}\left(m/s\right)\)
Mà vật đang chuyển động the chiều dương: \(v=0,08\sqrt{2}\left(m/s\right)\)
Gia tốc vật:
\(a=-\omega^2x=-2^2\cdot\left(-2\right)=8cm/s^2\)

Để tính quãng đường đi được, ta sử dụng công thức sau:
Quãng đường đi được = |x(t2) - x(t1)|
Với t2 = 13/6 s và t1 = 0, ta có:
x(t2) = 10cos(2π(13/6) - π/3) cm x(t1) = 10cos(2π(0) - π/3) cm
Thay vào công thức, ta tính được quãng đường đi được.
Với phương trình x = 20cos(10πt + π/6) cm, ta cần tính thời điểm vật đi qua vị trí M có li độ 10 cm lần thứ 2023.Để tính thời điểm vật đi qua vị trí M, ta sử dụng công thức sau:
t = (1/10π)arccos((x - 10)/20) - π/6
Thay vào công thức, ta tính được thời điểm vật đi qua vị trí M lần thứ 2023.
Vậy, ta đã giải được bài toán.