Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Số cách chọn là:
\(C^1_6\cdot C^9_{14}+C^2_6\cdot C^8_{14}=57057\left(cách\right)\)
a.
Xác suất: \(P=0,9.0,8.0,6=...\)
b.
Xác suất để 3 xạ thủ bắn trượt lần lượt là: 0,3; 0,4; 0,5
Xác suất để cả 3 cùng bắn trượt: \(0,3.0,4.0,5\)
Xác suất để ít nhất 1 người bắn trúng: \(P=1-0,3.0,4.0,5=...\)
Đáp án A
Lấy ngẫu nhiên từ ngân hàng đề thi 4 câu hỏi để lập một đề thi
có C 20 4 = 4845 đề thi.
Thí sinh A rút ngẫu nhiên được 1 đề thi có 2 câu đã thuộc
có C 10 2 . C 10 2 = 2025 trường hợp.
Thí sinh A rút ngẫu nhiên được 1 đề thi có 3 câu đã thuộc
có C 10 3 . C 10 1 = 1200 trường hợp.
Thí sinh A rút ngẫu nhiên được 1 đề thi có 4 câu đã thuộc
có C 10 4 = 210 trường hợp.
Do đó, thí sinh A rút ngẫu nhiên được 1 đề thi có ít nhất 2 câu đã thuộc
có 2025 + 1200 + 210 = 3435 trường hợp.
Vậy xác suất để thí sinh A rút ngẫu nhiên được 1 đề thi có ít nhất 2 câu đã thuộc là
3435 4845 = 229 323
Đáp án A
Lấy ngẫu nhiên từ ngân hàng đề thi 4 câu hỏi để lập một đề thi có C 20 4 = 4845 đề thi.
Thí sinh A rút ngẫu nhiên được 1 đề thi có 2 câu đã thuộc
có C 10 2 . C 10 2 = 2025 trường hợp.
Thí sinh A rút ngẫu nhiên được 1 đề thi có 3 câu đã thuộc
có C 10 3 . C 10 1 = 1200 trường hợp.
Thí sinh A rút ngẫu nhiên được 1 đề thi có 4 câu đã thuộc
có C 10 4 = 210 trường hợp.
Do đó, thí sinh A rút ngẫu nhiên được 1 đề thi có ít nhất 2 câu đã thuộc
có 2025 + 1200 +210 =3435 trường hợp.
Vậy xác suất để thí sinh A rút ngẫu nhiên được 1 đề thi có ít nhất 2 câu đã thuộc là
3435 4845 = 229 323
Đáp án B.
+ Rút ra 4 câu bất kì 
Có 
cách.
+ Rút ra 4 câu mà không có câu nào học thuộc 
Có 
cách.
Xác suất để bạn đó rút được 4 câu trong đó có ít nhất một câu đã học là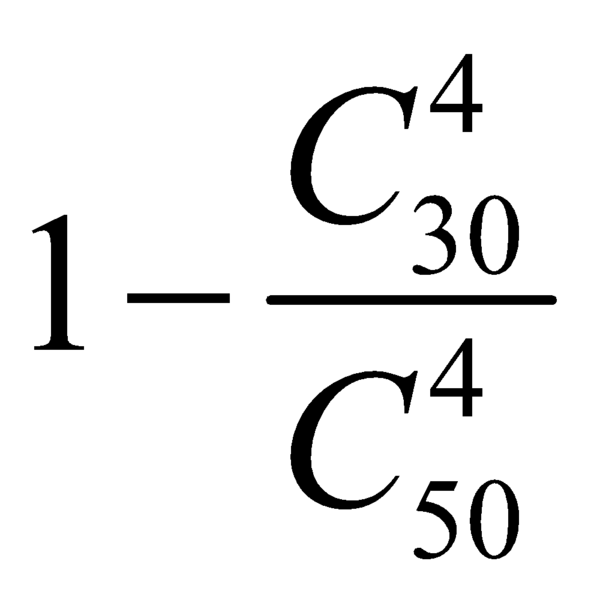 
*Giải bài toán*
Gọi số hạng đầu là \(a_1\) và công sai là \(d\). Số hạng tổng quát là \(a_n = a_1 + (n-1)d\).
*Điều kiện 1*
Tổng số báo danh của 5 học sinh đứng giữa hàng là gấp 5 lần số báo danh của học sinh đứng thứ 8:
\[a_6 + a_7 + a_8 + a_9 + a_{10} = 5a_8\]
\[5a_1 + 35d = 5(a_1 + 7d)\]
Điều này luôn đúng.
*Điều kiện 2*
Tổng số báo danh của học sinh ở vị trí chẵn bằng 3 lần tổng số báo danh của học sinh ở vị trí lẻ:
\[S_{chẵn} = 3S_{lẻ}\]
Với \(n = 22\), ta có:
\[S_{chẵn} = a_2 + a_4 + ... + a_{22}\]
\[S_{lẻ} = a_1 + a_3 + ... + a_{21}\]
\[11a_1 + 110d = 3(11a_1 + 55d)\]
\[11a_1 + 110d = 33a_1 + 165d\]
\[22a_1 = -55d\]
\[2a_1 = -5d\]
*Điều kiện 3*
\[S_3 - S_4 = 2025\]
Với \(n = 22\), \(k = 7\), \(l = 5\):
\[S_3 = 7a_1 + 77d\]
\[S_4 = 5a_1 + 55d\]
\[2a_1 + 22d = 2025\]
*Điều kiện 4*
\[a_{22} - a_{11} = 11d\]
\[11d = 11d\]
\[n = 22\]
*Tìm \(a_1\) và \(d\)*
Từ \(2a_1 = -5d\) và \(2a_1 + 22d = 2025\):
\[2a_1 = -5d\]
\[-5d + 22d = 2025\]
\[17d = 2025\]
\[d = \frac{2025}{17} = 119\]
\[2a_1 = -5 \cdot 119\]
\[a_1 = -\frac{595}{2}\]
*Kết quả*
\[n = 22\]
\[a_1 = -\frac{595}{2}\]
\[d = 119\]
Đáp án A
Số cách sắp xếp 50 câu cho một đề thi là 50!
Số cách chọn 20 câu nhận biết để xếp chúng vào đầu tiên là: 20!
Số cách chọn 10 câu thông hiểu để xếp chúng vào vị trí thứ hai là 10!
Số cách chọn 15 câu vận dụng để xếp chúng vào vị trí thứ ba là 15!
Số cách chọn 5 câu vận dụng cao xếp chúng vào vị trí cuối cùng là 5!
=> Xác suất cần tìm được tính bằng: P = 20 ! . 10 ! . 15 ! . 5 ! 50 ! = 4,56.10-26
=> Chọn phương án A.