Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Độ dài cạnh là \(\sqrt{32}=4\sqrt{2}\left(cm\right)\)
Diện tích xung quanh của hình lập phương là:
\(4\cdot\left(4\sqrt{2}\right)^2=4\cdot32=128\left(cm^2\right)\)

`1,`
S một đáy của hình lập phương đó là:
`144 \div 4 = 36 (m^2)`
Độ dài cạnh của hình lập phương đó là:
\(\sqrt {36} = 6(m)\)
Vậy, độ dài cạnh của hình lập phương đó là `6 m`.
`2,`
P đáy của hình hộp chữ nhật đó là:
`2(5+6)=2*11=22(m^2)`
Chiều cao của hình hộp chữ nhật đó là:
`154 \div 22=7 (m)`
Vậy, độ dài của chiều cao hình hộp chữ nhật đó là `7m.`

Vì là \(a^3\) nên mình dùng nthe ;-; với lại cũng có học căn nên mình làm vậy, còn nếu mà không được thì cho mình sửa:
Thể tích của hình lập phương đó là \(125m^3\)
Mà \(125=5^3\)
\(\Rightarrow\) Độ dài 1 cạnh của hình lập phương đó là \(5m\)
Độ dài cạnh là \(\sqrt[3]{125}=5\left(m\right)\)
Diện tích xung quanh là:
5^2*4=100(m2)

Độ dài cạnh của hình lập phương là \(\sqrt[3]{729}=9\left(cm\right)\)
Diện tích xung quanh của hình lập phương là \(4.9^2=324\left(cm^2\right)\)
Diện tích toàn phần của hình lập phương là \(6.9^2=486\left(cm^2\right)\)
Thể tích của hình lập phương đề bài đã cho là \(729cm^3\)
Lớp 7 đã học dạng \(\sqrt[3]{729}\) đâu nhỉ, theo em nên viết:
Vì \(9\cdot9\cdot9=729\) nên cạnh hình vuông là 9cm

a) Thể tích hình lập phương là: 4 . 4 . 4 = 64 (cm3)
b) Độ dài cạnh hình lập phương mới là: 4 . 3 = 12 (cm)
Thể tích hình lập phương mới là: 12 . 12 .12 = 1728 (cm3)
c) Thể tích hình lập phương mới gấp số lần thể tích hình lập phương ban đầu là: 1728 : 64 = 27 (lần)

Ta có:
Thể tích của hình lập phương là:
\(V = a^{3} = 343 \&\text{nbsp};\text{cm}^{3}\)=> Tìm cạnh \(a\) bằng cách lấy căn bậc ba của 343:
\(a = \sqrt[3]{343} = 7 \&\text{nbsp};\text{cm}\)1. Diện tích toàn phần của hình lập phương:
\(S_{t p} = 6 a^{2} = 6 \times 7^{2} = 6 \times 49 = 294 \&\text{nbsp};\text{cm}^{2}\)2. Diện tích xung quanh của hình lập phương:
\(S_{x q} = 4 a^{2} = 4 \times 7^{2} = 4 \times 49 = 196 \&\text{nbsp};\text{cm}^{2}\)Kết luận:
- Diện tích toàn phần: \(294 \&\text{nbsp};\text{cm}^{2}\)
- Diện tích xung quanh: \(196 \&\text{nbsp};\text{cm}^{2}\)
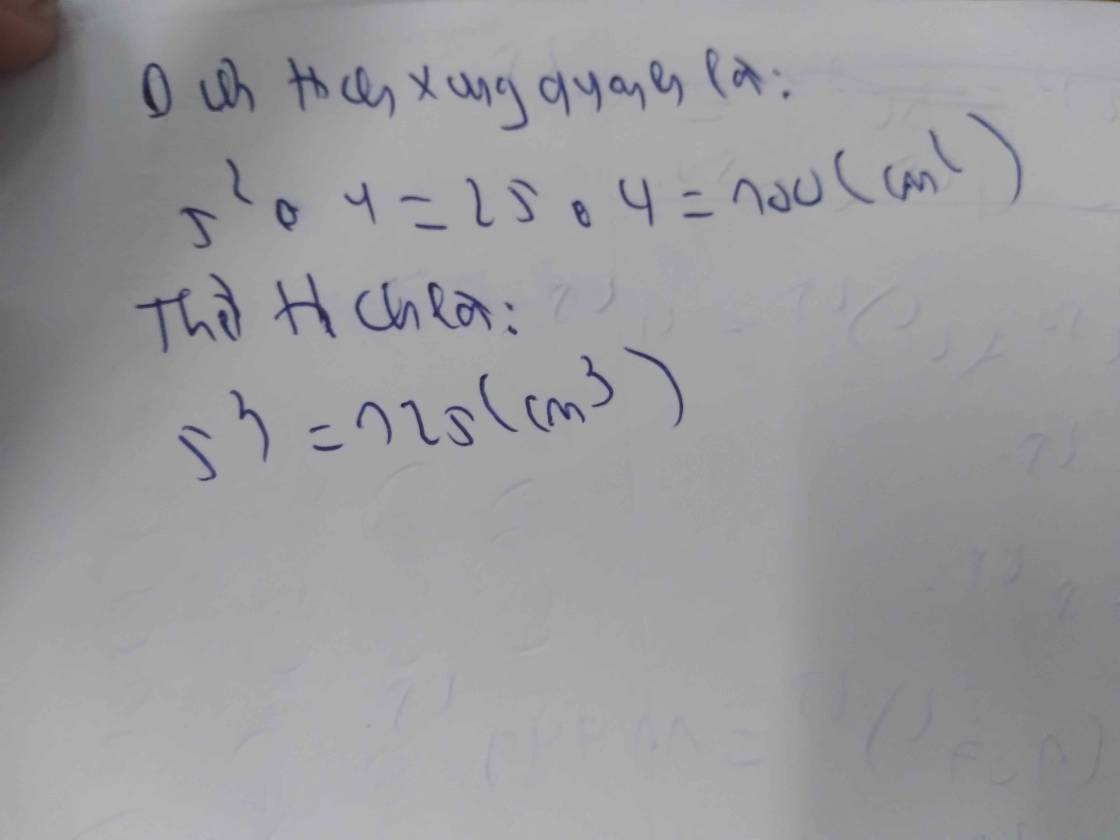
Diện tích xung quanh hình lập phương là: \(S = 4{a^2}\)
\(\begin{array}{l} \Rightarrow 100 = 4{a^2}\\ \Rightarrow {a^2} = 100:4\\ \Rightarrow a = 5\left( {cm} \right)\end{array}\)
Thể tích hình lập phương đó là:
\(V = {a^3} = {5^3} = 125\left( {{m^3}} \right)\)