
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Xét tứ giác ABCD có:
\(\begin{array}{l} \widehat A + \widehat B + \widehat C + \widehat D = {360^0}\\{85^0} + x + {65^0} + {75^0} = {360^0}\\x = {360^0} - {85^0} - {65^0} - {75^0} = {135^0}\end{array}\)

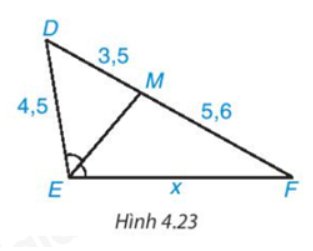
Trong Hình 4.23 có \(\widehat {DME} = \widehat {MEF}\) nên EM là tia phân giác của \(\widehat {{\rm{DEF}}}\).
Áp dụng tính chất đường phân giác của tam giác, ta có:
\(\dfrac{{E{\rm{D}}}}{{EF}} = \dfrac{{M{\rm{D}}}}{{MF}}\) hay \(\dfrac{{4,5}}{x} = \dfrac{{3,5}}{{5,6}}\)
Suy ra: \(x = \dfrac{{5,6.4,5}}{{3,5}} = 7,2\)(đvđd)
Vậy x = 7,2 (đvđd).

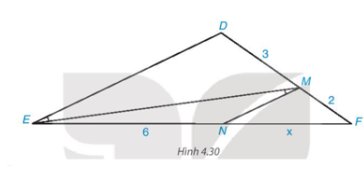
Trong Hình 4.30 có \(\widehat {DEM} = \widehat {EMN}\) mà hai góc này ở vị trí so le trong nên MN // DE.
Áp dụng định lí Thalès vào tam giác DEF có MN // DE, ta có:
\(\dfrac{{MF}}{{M{\rm{D}}}} = \dfrac{{NF}}{{NE}}\) hay \(\dfrac{2}{3} = \dfrac{x}{6}\)
Suy ra \(x = \dfrac{{2.6}}{3} = 4\) (đvđd).
Vậy x = 4 (đvđd).

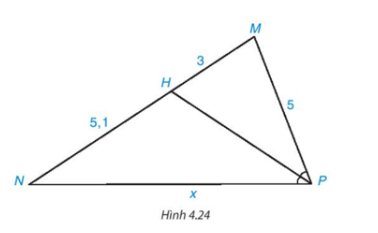
Trong Hình 4.24 có \(\widehat {MPH} = \widehat {NPH}\) nên PH là tia phân giác của \(\widehat {MPN}\).
Áp dụng tính chất đường phân giác của tam giác, ta có:
\(\dfrac{{MP}}{{NP}} = \dfrac{{MH}}{{NH}}\) hay \(\dfrac{5}{x} = \dfrac{3}{{5,1}}\)
Suy ra \(x = \dfrac{{5.5,1}}{3} = 8,5\) (đvđd).
Vậy x = 8,5 (đvđd).

a: Xét tứ giác DIHK có
góc DIH=góc DKH=góc KDI=90 độ
nên DIHK là hình chữ nhật
b: Xét tứ giác IHAK có
IH//AK
IH=AK
Do đó: IHAK là hình bình hành
=>B là trung điểm chung của IA và HK
Xét ΔIKA có IC/IK=IB/IA
nên BC//KA
Xét ΔIDA có IB/IA=IM/ID
nên BM//DA
=>B,C,M thẳng hàng

a: Xét ΔABC có F,E lần lượt là trung điểm của AB,AC
=>FE là đường trung bình của ΔABC
=>FE//BC và \(FE=\frac12BC\)
=>BFEC là hình thang
Hình thang BFEC có \(\hat{FBC}=\hat{ECB}\) (ΔABC cân tại A)
nên BFEC là hình thang cân
b: Xét ΔABC có
F,D lần lượt là trung điểm của BA,BC
=>FD là đường trung bình của ΔABC
=>FD//AC và \(FD=\frac{AC}{2}\)
Xét ΔMAC có
I,K lần lượt là trung điểm của MA,MC
=>IK là đường trung bình củaΔMAC
=>IK//AC và \(IK=\frac{AC}{2}\)
Ta có: FD//AC
IK//AC
Do đó: FD//IK
Ta có: \(FD=\frac{AC}{2}\)
\(IK=\frac{AC}{2}\)
Do đó: FD=IK
Xét tứ giác FDKI có
FD//IK
FD=IK
Do đó: FDKI là hình bình hành
c: HK=HM+KM
\(=\frac12\cdot\left(MB+MC\right)=\frac12\cdot BC\)
=FE
Xét tứ giác FEKH có
FE//KH
FE=KH
Do đó: FEKH là hình bình hành
=>FK cắt EH tại trung điểm của mỗi đường(1)
FDKI là hình bình hành
=>FK cắt DI tại trung điểm của mỗi đường(2)
Từ (1),(2) suy ra FK,EH,DI đồng quy
d: ΔABC đều
mà AD là đường trung tuyến
nên AD là phân giác của góc BAC và AD⊥BC
=>\(\hat{BAD}=\frac12\cdot\hat{BAC}=\frac12\cdot60^0=30^0\)
Xét tứ giác APMD có \(\hat{APM}+\hat{ADM}=90^0+90^0=180^0\)
nên APMD là tứ giác nội tiếp đường tròn đường kính AM
=>APMD nội tiếp (I)
Xét (I) có \(\hat{PAD}\) là góc nội tiếp chắn cung PD
=>\(\hat{PID}=2\cdot\hat{PAD}=60^0\)
Xét ΔIPD có IP=ID và \(\hat{PID}=60^0\)
nên ΔIPD đều
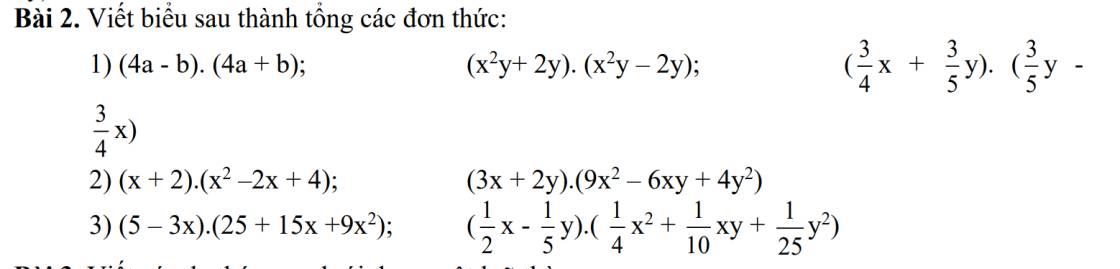 mong
mong 







Bài 1 : (4a - b).(4a + b) = 16a2 + (-b2)
(\(x^2y\) + 2y)(\(x^2\)y - 2y = \(x^4\).y2 + (- 4y2)
(\(\dfrac{3}{4}\)\(x\) + \(\dfrac{3}{5}\)y)(\(\dfrac{3}{5}\)y - \(\dfrac{3}{4}\)\(x\)) = \(\dfrac{9}{25}\)y2 + (- \(\dfrac{9}{16}\)\(x^2\))
2; (\(x+2\))(\(x^2\) - 2\(x\) + 4) = \(x^3\) + 8
(3\(x\) + 2y)(9\(x^2\) - 6\(xy\) + 4y2) = 27\(x^3\) + 8y3
3, (5- 3\(x\))(25 + 15\(x\) + 9\(x^2\)) = 125 + ( -27\(x^3\))
(\(\dfrac{1}{2}\)\(x\) - \(\dfrac{1}{5}\)y).(\(\dfrac{1}{4}\)\(x^2\) + \(\dfrac{1}{10}\)\(xy\) + \(\dfrac{1}{25}\)y2 = \(\dfrac{1}{8}\)\(x^3\) + (-\(\dfrac{1}{125}\)y3)
em cảm ơn cô ạ